Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nalezení obecné reálné funkce splňující předepsanou rovnici (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 07. 2011 10:50
- archipatelin
- Příspěvky: 36
- Reputace: 1
Nalezení obecné reálné funkce splňující předepsanou rovnici
Jak vypadá obecná realná funkce jedné reálné proměnné 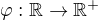 splňující rovnici:
splňující rovnici: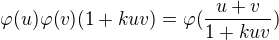 ,
,
kde  je libovolná reálná konstanta?
je libovolná reálná konstanta?
Našel jsem dvě speciální řešeni. Jedno za předpokladu, že  je sudá funkce:
je sudá funkce:
a druhe pro 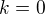 :
: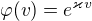 , kde
, kde 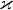 je libovolná reálná konstanta.
je libovolná reálná konstanta.
Ale tyto řešeni nejsou totožná (pro nulové  ), tak ani jedno z nich nemůže být obecné!
), tak ani jedno z nich nemůže být obecné!
Jak najít obecné řešení?
Děkuji za pomoc.
Offline
- (téma jako vyřešené označil(a) archipatelin)
#2 25. 07. 2011 11:25
- archipatelin
- Příspěvky: 36
- Reputace: 1
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
Doplňující dotaz.
Je exponenciální funkce 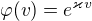 jediná (tj. nejobecnější) funkce splňující identitu:
jediná (tj. nejobecnější) funkce splňující identitu: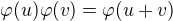
(vynechme triviální připad  ) ?
) ?
Offline
#3 25. 07. 2011 11:46
- archipatelin
- Příspěvky: 36
- Reputace: 1
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
Právě se mi podařilo najít toto řešení: ,
,
ale navim jak dokázat, že se jedná o řešení obecne!
Offline
#4 25. 07. 2011 21:08
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ archipatelin:
Možná by se to dalo dokázat postupem, kterým jsi na toto řešení přišel.
"Máte úhel beta." "No to nemám."
Offline
#5 25. 07. 2011 21:14
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ archipatelin:
Zapsal bych si vztahy pro  . Např. je buď
. Např. je buď 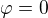 nebo je
nebo je 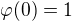 a
a  (z toho jsi asi odvodil vztah pro sudou
(z toho jsi asi odvodil vztah pro sudou  ).
).
Jak jsi prosím odvodil poslední vztah (se sinh)?
"Máte úhel beta." "No to nemám."
Offline
#6 25. 07. 2011 22:38
- archipatelin
- Příspěvky: 36
- Reputace: 1
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
check_drummer napsal(a):
Jak jsi prosím odvodil poslední vztah (se sinh)?
Rozdělil jsem  na součet její sudé a liché části:
na součet její sudé a liché části: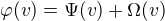

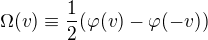
Pro speciální připad 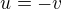 plati:
plati: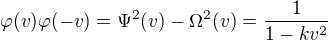 ,
,
tak  .
.
Pro 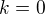 ze znalosti speciálního řešení
ze znalosti speciálního řešení 
plyne 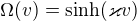 .
.
Pak stačí jen ověřit (pracně), že vztah splňuje rovnici pro obecné  .r
.r
Offline
#7 26. 07. 2011 18:16
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ archipatelin:
Proč nemůže být před odmocninou znaménko mínus?
I kdybychom ověřili, že uvedený vztah splňuje výše uvedenou rovnici, dle mého to ještě neznamená, že žádná jiná funkce uvedenou rovnost splňovat nemůže.
(Myslím, že si úloha zaslouží přesunutí do Zajímavých úloh z VŠ.)
"Máte úhel beta." "No to nemám."
Offline
#8 26. 07. 2011 18:47
- archipatelin
- Příspěvky: 36
- Reputace: 1
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
check_drummer napsal(a):
Proč nemůže být před odmocninou znaménko mínus?
Obor hodnot hledané funkce je 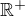 ,což znaménko mínus před odmocninou nesplňuje (a vlastně ani triviální připad
,což znaménko mínus před odmocninou nesplňuje (a vlastně ani triviální připad 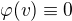 ).
).
Nalezené řešení platí pro všechna  to jsem dokázal.Ale zda je to řešení obecné, to je ta má otázka z níž si nevím rady.
to jsem dokázal.Ale zda je to řešení obecné, to je ta má otázka z níž si nevím rady.
S tím souvisí jestli se dá nějak dokázat,že exponenciála je jedinou funkcí splňující identitu: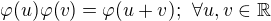
?
Offline
#9 26. 07. 2011 19:40
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
archipatelin napsal(a):
Doplňující dotaz.
Je exponenciální funkcejediná (tj. nejobecnější) funkce splňující identitu:
(vynechme triviální připad) ?
myslim, že ne, že by šlo třeba volit jinou konstantu 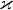 pro
pro 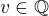 a jinou pro
a jinou pro 
Offline
#10 26. 07. 2011 20:00
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ Stýv:
To asi nepůjde (jestli jsem pochopil tvou myšlenku správně), protože součet dvou iracinálních čísel není vždy iracionální.
"Máte úhel beta." "No to nemám."
Offline
#11 26. 07. 2011 20:07
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ archipatelin:
Má-li však být  opravdu definována pro všechna u z
opravdu definována pro všechna u z  , pak tvá funkce není definována pro
, pak tvá funkce není definována pro  .
.
"Máte úhel beta." "No to nemám."
Offline
#12 26. 07. 2011 20:19
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ check_drummer: pravda, tak jednoduchý to nebude, nicméně když si zvolim třeba f(1)=e, pak z toho plyne f(x)=exp(x) pro racionální x, ale pro iracionální x ne (imho). tudíž si můžu zvolit třeba f(pi)=exp(pi/2) a z toho odvodit f(p*pi+q) pro p,q racionální atd... nebo to někde selže? ruku do ohně bych za to, pravda, nedal:)
Offline
#13 26. 07. 2011 21:37
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ Stýv:
Takhle na první pohled by to mohlo fungovat (ale taky bych si teď nechtěl hrát s ohněm :-). Po "vyřízení" pi bys tedy asi přidal nějaké další iracinální číslo x, pro které f ještě není definovaná, a definoval hodnoty f(p*pi+r*x+r) pro p,q,r racionální? Akorát nevím, jestli by pro takovou definici bylo možné použít indukci - tj. nechť je pro n iracionálních čísel (a jejich kombinace) f již definována... tady by n nebylo přirozené a tudíž by asi šlo o nějakou transfinitní indukci... A pak bychom přidali n+1-ní...
OT: Nevím, přiznám se, že jsem si otevřel slivovici a není vůbec dobrá. :-) Snad jsem neporušil nějaká pravidla fóra. (Návštěvník má být střízliv, řádně upraven a oholen.)
"Máte úhel beta." "No to nemám."
Offline
#14 26. 07. 2011 23:36 — Editoval archipatelin (26. 07. 2011 23:40)
- archipatelin
- Příspěvky: 36
- Reputace: 1
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ check_drummer:, ↑ Stýv:
Hoši, přesně nevím co tím postupným dodefinováním zamýšlíte, ale možná vás bude zajímat, že za předpokladu spojitosti funkce 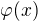 .
.
Je 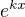 jediná funkce splňující identitu
jediná funkce splňující identitu .
.
Požadavek  pak definuje exponenciálu jednoznačně.
pak definuje exponenciálu jednoznačně.
Je to jeden ze způsobů jak definovat exponenciální funkci.
viz Hewitt and Stromberg, 1965
Offline
#15 27. 07. 2011 00:43
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ archipatelin: za předpokladu spojitosti je to jednoduchý. bez něj je to zajímavější;)
Offline
#16 27. 07. 2011 09:26
- archipatelin
- Příspěvky: 36
- Reputace: 1
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ Stýv:
Zapoměl jsem zmínit předpoklad, že funkce  je spojítá, resp. spojitá až na konečný počet bodů.
je spojítá, resp. spojitá až na konečný počet bodů.
Na té wiki píší, že je-li funkce s touto vlastností spojitá někde pak je spojitá všude. Proto příkladem jiné funkce než exponenciály, která by splňovala "exponenciální" identitu musí být funkce která není nikde spojitá.
Offline
#17 27. 07. 2011 20:02
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ archipatelin:
A jak je to s jejím definičním oborem? Má být definována pro všechna reálná čísla či nikoli?
U zápisů jako 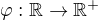 si nikdy nejsem jist, zda je tím automaticky dán i definiční obor nebo jen jeho "nadmnožina".
si nikdy nejsem jist, zda je tím automaticky dán i definiční obor nebo jen jeho "nadmnožina".
"Máte úhel beta." "No to nemám."
Offline
#18 27. 07. 2011 20:15
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ check_drummer: takhe napsaný je vlevo def. obor a vpravo nadmnožina oboru hodnot
Offline
#19 28. 07. 2011 08:11
- archipatelin
- Příspěvky: 36
- Reputace: 1
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ :Souhlasím, že tento zápis označuje za definiční obor celou množinu reálných čísel.
Ja však měl na mysli definiční obor jako nějakou podmnožinu  .
.
Omluvám se za tuto nejasnost.
Offline
#20 29. 07. 2011 09:35
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení obecné reálné funkce splňující předepsanou rovnici
↑ archipatelin:
Pak je otázka pro jaká u,v má být splněn tvůj vztah: pro všechna reálná, pro která není zlomek =0 a nebo pro všechna, kde všechny výrazy v argumentu hledané funkce jsou z jejího definičního oboru. Pokud jde o druhý případ, pak např. vyhovuje i funkce s prázdným definičním oborem nebo nějaké speciální podmnožiny R, apod.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nalezení obecné reálné funkce splňující předepsanou rovnici (TOTO TÉMA JE VYŘEŠENÉ)
