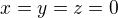Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 08. 2011 01:18
Průnik prostorů
Dobrý den,
studuji Olšákův Úvod do algebry, zejména a lineární a ve větě 1.22 je psáno, že průnik dvou lineární podprostorů N a M lin. prostoru L je také lineární podprostor. Na vyzkoušení je tam uveden příklad 1.21. Vyzkoušel jsem však kombinaci příkladů 1.20 a 1.21 a nedobral jsem se k tomuto závěru.
Konkrétně: M={(a,a,a); a € R) je lineární podprostor prostoru R3. N={(x,y,z); x+2y=0} je též lineární podprostor prostoru R3. Pokud však zvolím vektor v=(a,a,a), v prostoru N tento prvek není platný (očividně), pokud se nejedná o nulový vektor. Prosím o vysvětlění tohoto průniku lin. prostorů a co se při tom děje.
Děkuji.
Offline
#2 09. 08. 2011 03:30
Re: Průnik prostorů
Možná si pleteš průnik se sjednocením. V průniku jsou právě ty vektory, které patří do obou podprostorů zároveň. Jak jsi správně podotkl, bude průnik triviální podprostor 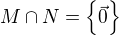 .
.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#5 09. 08. 2011 10:34
Re: Průnik prostorů
Ještě jedna otázka:
lineární podprostor musí přejímat operace násobení a sčítání ze svého nadprostoru, nebo může mít definované vlastní a pořád být podprostorem?
Uvažuji prostor všech kladných reálných čísel R+ s operacemi sčítaní x+y=abs(x+y) a násobení c*x=abs(c*x). Je takto definovaný prostor podprostorem všech reálných čísel? Nebo aby byl, musely by být operace jako podmínky, tzn R+ = {(x,y); x+y=abs(x+y) a c*x=(abs(c*x)}?
S pozdravem
NewRose
Offline
#6 09. 08. 2011 12:03
Re: Průnik prostorů
↑ NewRose: aby to byl podprostor, musí mít stejné operace. R+ není vektorovým prostorem nad tělesem R
Offline
#8 09. 08. 2011 13:45
#9 09. 08. 2011 14:21
Re: Průnik prostorů
↑ Stýv: Jo, toho jsem si taky všimnul... ale fakt, že v podmínkách v Olšákovi o existenci opačného prvku k jakémukoli prvku není podmínka pro lineární prostor, mě usvědčil k tvrzení že R+ je lineární prostor. Taky jsem se divil, ale dobrý... aspoň už je to jasný.
Offline
#10 09. 08. 2011 14:38
Re: Průnik prostorů
↑ NewRose: pokud tam není explicitně uvedená, tak bude vyplývat z ostatních
Offline
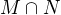 musí splňovat podmínky obou ->
musí splňovat podmínky obou ->  ?
?
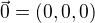 , pretoze z podmienky
, pretoze z podmienky  dostavame
dostavame  , co plati len pre
, co plati len pre  a teda
a teda