Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Základní škola
- » 4 boký Jehlan s podstavou obdelníka (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 08. 2011 15:14
4 boký Jehlan s podstavou obdelníka
Dobrý den, potřeboval bych poradit jak mám vypočítat příklad se 4 bokým jehlanem který má podstavnou hranu obdelníka , a = 24 , b = 13 , výška = 18 . Sp=? , Spl=?,S=?,V=? Potřeboval bych jen vědět co mám použít ve vzorečku v obsahu pláště. U čtvercové podstavy to je Spl = 4 * 1/2 * a * vs
ale u obdelníka mám přeci stranu a,b
předem děukuju za odpověď
Offline
- (téma jako vyřešené označil(a) Koucis)
#2 10. 08. 2011 15:33 — Editoval Oxyd (10. 08. 2011 16:05)
Re: 4 boký Jehlan s podstavou obdelníka
U obdélníkové podstavy je to podobné jako u té čtvercové. Plášť toho jehlanu je tvořený ze čtyř trojúhelníků, že? Obsah trojúhelníka spočítat umíš. Když je podstava čtvercová, tak jsou všechny čtyři trojúhelníky v plášti stejné -- proto 4 * 1/2 * a * vs. Protože máš ale obdélníkovou podstavu, tak nebudou všechny čtyři stejné -- bude to „dva a dva“ -- vždycky ty protější trojúhelníky jsou stejné.
Takže si stačí spočítat výšku trojúhelníka z pláště, který je „přilepený“ k hraně podstavy délky a -- z toho spočítáš jeho obsah. Pak si spočítej výšku trojúhelníka z pláště, který je „přilepený“ k hraně podstavy délky b, z toho zas spočítáš obsah tohohle trojúhelníku. A z toho už obsah pláště dopočítáš snadno.
Je samozřejmě vhodné si k tomu nakreslit obrázek.
Edit: Rozhodl jsem se konečně si pohrát s GeoGebrou. Teď se aspoň můžu vyjádřit přesněji -- trojúhelníky ABE a DCE jsou stejné (mají stejný obsah), trojúhelníky BCE a ADE mají rovněž stejný obsah. Stačí spočítat obsahy těhle trojúhelníků a výsledek je nasnadě.
OT: Rád bych na tomhle obrázku nějak zvýraznil, že úhly ESS_a, ESS_b jsou pravé -- dá se to v GeoGebře nějak hezky udělat?
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#3 10. 08. 2011 16:20 Příspěvek uživatele Koucis byl skryt uživatelem Koucis.
#4 10. 08. 2011 16:25
Re: 4 boký Jehlan s podstavou obdelníka
Tady je kdyžtak zadání Máme čtyřboký jehlan, který má podstavu obdélník s rozměry 24 cm, 13 cm. Výška jehlanu
je 18 cm. Vypočtěte : a) obsah podstavy b) obsah pláště
c) povrch jehlanu d) objem jehlanu
možná budu vypadat jako uplnej blbec ale počítám výšku stěny tg45° = 12/ró (aspoň takhle nás učí ve škole značit tuto výšku) na tg45° sem přišel příkladem 360°/4 a ró nám půlí stěnu na 45° .. trošku se do toho zamotávám ... tak doufám že mě pochopíš jak to myslim :) děkuju za radu
Offline
#5 10. 08. 2011 16:38 — Editoval Oxyd (10. 08. 2011 16:43)
Re: 4 boký Jehlan s podstavou obdelníka
Koucis napsal(a):
možná budu vypadat jako uplnej blbec ale počítám výšku stěny tg45° = 12/ró (aspoň takhle nás učí ve škole značit tuto výšku) na tg45° sem přišel příkladem 360°/4 a ró nám půlí stěnu na 45° .. trošku se do toho zamotávám ... tak doufám že mě pochopíš jak to myslim :) děkuju za radu
Chceš vypočítat výšku stěny, kterou jsem já označil jako  ? Na to tangens nepotřebuješ, stačí ti Pýthagorova věta. Znáš výšku jehlanu -- to je úsečka ES. (S je střed podstavy.) Také znáš délku úsečky
? Na to tangens nepotřebuješ, stačí ti Pýthagorova věta. Znáš výšku jehlanu -- to je úsečka ES. (S je střed podstavy.) Také znáš délku úsečky 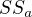 , přičemž
, přičemž  je střed hrany a -- její délka je půlka délky hrany b (protože je rovnoběžná s hranou b, ale jde jenom do středu podstavy, místo aby šla až na druhý konec, tj úsečku CD). Navíc je úhel
je střed hrany a -- její délka je půlka délky hrany b (protože je rovnoběžná s hranou b, ale jde jenom do středu podstavy, místo aby šla až na druhý konec, tj úsečku CD). Navíc je úhel  pravý. Takže máš pravoúhlý trojúhelník
pravý. Takže máš pravoúhlý trojúhelník  , znáš délky odvěsen a přepona je přesně úsečka
, znáš délky odvěsen a přepona je přesně úsečka 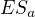 , neboli výška té jedné stěny. Dopočítáš to z tohohle?
, neboli výška té jedné stěny. Dopočítáš to z tohohle?
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#7 12. 08. 2011 16:18
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: 4 boký Jehlan s podstavou obdelníka
↑ Oxyd: V GeoGebře se pravé úhly automaticky graficky odlišují od kosých, ale ve tvém případě úhel pravý není (ve 2D smyslu), tak je tomu potřeba trochu pomoct.
Nejdřív bych vyznačil ten úhel (http://wiki.geogebra.org/en/Angle_Tool) a pak mu nastavil popisek (http://wiki.geogebra.org/en/Labels_and_Captions#Caption), třeba 90° nebo jen ●, tu tečku pak můžeš posunout, aby to nějak vypadalo.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Základní škola
- » 4 boký Jehlan s podstavou obdelníka (TOTO TÉMA JE VYŘEŠENÉ)