Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 08. 2011 02:51
Výpočet jízdní doby vlaku
Ahoj,
Mám problém s výpočtem jízdní doby jedoucího vlaku. Můj problém nastává v ten okamžik, kdy se vlak začíná rozjíždět z traťové omezené rychlosti - 70 km/h na maximální rychlost 100 km/h, přičemž se nestačí rozjet úplně, jelikož záhy začíná brzdit do stanice (zastavuje). Mým úkolem je určit na jakou maximální rychlost se stačí rozjet, aby stihl zastavit v daném místě stanice.
Znám tedy počáteční rychlost v0 = 70 km/h, dále koncovou rychlost = 0 km/h, celkovou dráhu, kterou urazí od pocatecniho do koncoveho bodu s = 782 m, zrychlení vlaku a = 0,35 m/s2 a zpomalení vlaku b = -0,5 m/s2. Již jsem nad tim stravil nejakej ten cas, ale zadne kloudné matematické řešení mne nenapadlo, budu velice rád, když mne někdo inteligentnější než jsem já pomůže. Díky moc
Offline
- (téma jako vyřešené označil(a) Jigfreed)
#2 27. 08. 2011 03:22
- OiBobik
- Moderátor
- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Výpočet jízdní doby vlaku
↑ Jigfreed:
vlak zřejmě bude zrychlovat až do času t1, kdy nastane max. rychlost v1=a*t1 a v ten okamžik začne zpomalovat až do času t2, kdy se zastaví, přičemž v celém procesu urazí dráhu s.
zřejmě musí platit
70+a*t1=-b*(t2-t1) ... (vlak musí zpomalit právě o tolik, o kolik zrychlil, a ještě o počáteční rychlost 70 kmh)
70t1+a*(t1^2)/2-(b*(t2-t1)^2)/2=s ... (vlak při zrychlování a zpomalování urazí právě vzdálenost s, zrychlení i zpomalení uvažujeme konstantní)
Z těchto dvou rovnic o dvou neznámých stačí zjistit hodnotu t1 a dosadit do "v1=a*t1";
(snad tam není chyba, přece jen je půl čtvrté ráno : )) )
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 27. 08. 2011 06:12 — Editoval Jigfreed (27. 08. 2011 06:16)
Re: Výpočet jízdní doby vlaku
↑ OiBobik: Moc si vazim toho, ze si se pokusil mi odpovedet, ale tohle mi hlava nebere respektive nedaří se mi tu druhou rovnici upravit do nějakého kloudného stavu(to je můj kámen úrazu). Asi zustanu u proverene metody pokus - omyl :) Ale díky
Offline
#4 27. 08. 2011 07:44
Re: Výpočet jízdní doby vlaku
↑ Jigfreed:
z grafu je vidět
(plocha pod grafem = dráha)
(obsah lichoběžníka + trojúhelníka)
protože dále platí
a
(tady je velikost 
)
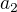dostaneš po dosazení
v této rovnici je jediná neznámá 
, vypočítat ji by neměl být problém (pozor na jednotky)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 27. 08. 2011 14:00
Re: Výpočet jízdní doby vlaku
↑ zdenek1:Super, díky moc, už to vychází. Jediná věc, která mi uplně není jasná je, jaktože v první rovnici počítáme s dráhou jako s plochou pod grafem, když by to ve skutečnosti měla být přímka rovnající se t1 a t2?
Offline
#6 27. 08. 2011 15:34
Re: Výpočet jízdní doby vlaku
↑ Jigfreed:
Představ si, že rychlost bude konstantní. (třeba v0).
Pak v tom grafu od ↑ zdenek1: to bude rovnoěžka s osou t.
No a jak známo tak platí s=v0*t0 (ujetá dráha je rychlost x doba jízdy).
Což je ovšem také plocha obdélníku o stranách t0 a v0.
Offline