Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 09. 2011 22:13
Tangens
Mám vypočítaný příklad. Rád bych požádal o jeho kontrolu a radu jaký je vlastně výsledek.
tg^2 alfa + 2 tg alfa = 3
substituce: tg alfa = y
y^2 + 2y - 3 = 0
D = 4
y1 = 1
y2 = -3
Mám dva výsledky, který je ten správný, nebo jsou to oba?? a je toto konečný výsledek?? Díky
Offline
#2 25. 09. 2011 22:24 — Editoval found (25. 09. 2011 22:24)
Re: Tangens
Tohle ještě není výsledek, jestli se nepletu, ty chceš spočíst, kolik je alfa, ale získal jsi jen y, teď musíš řešit následující dvě rovnice:
Jinak rovnice máš dobře, akorát Diskriminant máš špatně  Ty máš už odmocninu z diskriminantu jako 4.
Ty máš už odmocninu z diskriminantu jako 4.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#4 25. 09. 2011 22:42
Re: Tangens
↑ Jain:
Já bych to udělal na kalkulačce :-), určité u druhé rovnice.
Ta první jde i přes tabulky, kde najdeš hodnotu:
Jde o to, že tangens je definováno jako sínus dělené cosínem. To znamená, že aby se výraz rovnal jedna, musí se rovnat sinus cosínu. A to nastává pro případ 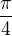 , kdy se hodnoty obou funkcí rovnají
, kdy se hodnoty obou funkcí rovnají 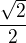 a poté pro
a poté pro  , kdy se obě funkce rovnají
, kdy se obě funkce rovnají  . A samozřejmě nesmíme zapomenout na periodu.
. A samozřejmě nesmíme zapomenout na periodu.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
