Matematické Fórum

jiskra · 18. 10. 2011 11:33 — Editoval jiskra (18. 10. 2011 12:31)

mam priklad :
Mejme Vektorovy prostor P3={a0 + a1x + a2x^2: a0, a1 ,a2 patri do R} . Rozhodnete o linearni zavislosti ci nezavislosti polynomu:
p(x)= x+2
q(x)= x^2 - x
r(x)= x^2 - 2

vim:
- ze linearne zavisly je pokud je vysledek rovny nule
- ze bych mel vytvorit soustavu rovnic a upravit je do trojuhelnikoveho tvaru a urcit jestli je prave jedno reseni a vsechny rovnice v soustave maji vysledek nula( pak je linearne zavisla)

nevim:
jak vlastne vytvorim tu soustavu rovnic ?

Jelena (úprava): text z příspěvky 3 (smazáno):

Ne, je to zadani z vysoke, ale ja nikdy vektorove prostory nebral. takze co vim je pouze to co jsem precetl z pdf/webu.

Jiskra (úprava): děkuji za presun. byl jsem presvedceny ze pisu do kategorie vysoka skola.

vanok · 18. 10. 2011 13:22

Ahoj ↑ jiskra:,

Mozes vyjadrit tvoje vektory v kanonickej baze z P3 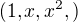$(1,x, x^2,)$
(POZOR NA PORIADOK a pis aj nuly)
a vyjadri podmienku nat studium zavislosti-nezavislosti tvojich "vektorov "
co ta dovedie k jednej matici ....

POZOR v tvojom texte su nepresnosti:

jiskra napsal(a):
- ze linearne zavisly je pokud je vysledek rovny nule

oprav to podla tvojich poznamok z poslucharne

Srdecne Vanok

jiskra · 18. 10. 2011 13:53

vanok napsal(a):
POZOR v tvojom texte su nepresnosti:
jiskra napsal(a):
- ze linearne zavisly je pokud je vysledek rovny nule
oprav to podla tvojich poznamok z poslucharne

bud jsem to spatne napsal nebo pochopil.
vychazel jsem odtud. http://www.aristoteles.cz/matematika/li … ektoru.php
na vysce to budeme teprve brat, ted to mame pouze spocitat jako domaci ukol.

u P3 me matlo scitani {a0 + a1x + a2x^2: a0, a1 ,a2 patri do R}
muzu tedy udelat z
p(x)= x+2
q(x)= x^2 - x
r(x)= x^2 - 2 tohle? :

matici:
1 0 2
-1 1 0
0 1 -2
GeM:
1 0 2
0 1 2
0 0 -4

A co znamena "vyjadri podmienku nat studium zavislosti-nezavislosti tvojich "vektorov " " ?

Rumburak

↑ jiskra:
Definice lineární závislosti / nezávislosti vektorů je i v odkazovaném webovém materiálu bohužel vyslovena nepřesně.
Raději hledej v literatuře doporučené učitelem.

jiskra · 20. 10. 2011 11:03

co teda mam vlastne delat s tim prikladem?

vanok · 20. 10. 2011 11:18 — Editoval vanok (20. 10. 2011 11:52)

↑ jiskra:

Upresni v akej baze pracujes???
Ja som ti navrhol tuto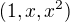

$(1,x, x^2)$

Vyuzi ucinne tvoje prednasky a najma tvoje poznamky

Tak daj to do poriadku

Srdecne Vanok

Upravena o 11 49 (20/10/2011)

Rumburak

↑ jiskra:
Především správně porozumět definici lineární závislosti a nezávislosti:

Mějme lin. prostor $V$ nad tělesem $T$ a vektory

(1) $\vec{u}_1, ... , \vec{u}_n \in V$ .

Sestavme rovnici

(2) $x_1 \vec{u}_1 + ... + x_n \vec{u}_n = \vec 0$

pro neznámé 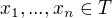$x_1, ... , x_n \in T$ . Tato rovnice má vždy alespoň tzv. triviální řešení $x_1 = x_2= ... = x_n = 0$ .
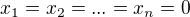Důležitou otázkou je, zda rovnice (2) má vedle tohoto triviálního řešení ještě nějaké další řešení , v němž by už bylo
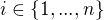$x_i \ne 0$ pro některé $i \in \{1, ... , n\}$ (tzv. netriviální řešení).

Pokud ANO, pak říkáme, že vektrory (1) jsou lineárně závislé.

Pokud NE, pak říkáme, že vektrory (1) jsou lineárně nezávislé.

Ta heslovitá "definice" zde je opravdu špatně, protože je nepřesná.

vanok · 20. 10. 2011 11:54 — Editoval vanok (20. 10. 2011 11:54)

↑ Rumburak:
Mas pravdu ze treba pouzivat presnu definiciu, nebolo by uzitocne dat taketo dokonale diela ako tvoj posledny prispevok do nejakej data banky

Srdecne Vanok

Rumburak · 20. 10. 2011 12:22

↑ vanok:
No o tom jsem nikdy nepřemýšlel, nenapsal jsem zde nic nového.
Pokud by to někdo chtěl někam zařadit, nemám žádné námitky. :-)

vanok · 20. 10. 2011 12:31

↑ Rumburak:
No take nieco aby sme nemuseli sa stale opakovat

Rumburak · 20. 10. 2011 13:33

↑ vanok:
Rozumím, ale jsem poněkud skeptický. Problém nevidím v tom, že by zdroje informací neexistovaly, ale spíše v neznalosti, jak se k nim dostat,
nebo dokonce i v neochotě je prohledávat a využívat. Když hledám neznámou ulici, mohu se buďto podívat do plánu města nebo se někoho zeptat -
většina lidí volí druhou možnost a zde je to, myslím, podobné.

vanok · 20. 10. 2011 13:37 — Editoval vanok (20. 10. 2011 13:37)

↑ Rumburak:
uhm, vidim ze medzi inym treba byt aj velky psycholog :-)

jiskra · 20. 10. 2011 14:08

Rumburak: dekuji snad uz to chapu lepe

vanok: predpokladam ze tuto (1,x, x^2) , kdyz P3={a0 + a1x + a2x^2: ...)

porad nevim co dal... z materialu jsem spis zmatenejsi nez pred tim.

jiskra · 20. 10. 2011 14:12

Rumburak napsal(a):
↑ vanok:
Rozumím, ale jsem poněkud skeptický. Problém nevidím v tom, že by zdroje informací neexistovaly, ale spíše v neznalosti, jak se k nim dostat,
nebo dokonce i v neochotě je prohledávat a využívat. Když hledám neznámou ulici, mohu se buďto podívat do plánu města nebo se někoho zeptat -
většina lidí volí druhou možnost a zde je to, myslím, podobné.

nez jsem tu napsal hledal jem 4 hodiny na netu vsude mozne. vektory mi nic moc nerikaji, takze tezko rozlisim uzitecne a spatne informace.
ne ze bych se nesnazil.

4hodiny "zbytecneho" hledani neznalnce > nez 4 min znalce

Rumburak · 20. 10. 2011 15:21

↑ jiskra:
Tu úvahu o sklonu mnohých lidí raději se zeptat než samostatně hledat jsem mínil spíše všeobecně.
Net není špatný, ale není tam všechno a ne všechno je tam správně. Učebnice, skripta nebo i pečlivé zápisy z přednášek bývají lepší.

K úloze: Zda jsou vektory lin. závislé či nezávislé není určeno volbou báze, o tu se vůbec nemusíš starat, nechceš-li (i když znalost báze
může řešení takové úlohy usnadnít). Postačí, když se budeš držet mého návodu v ↑ Rumburak: . Nastíním to podrobněji:

Jsme v prostoru polynomů stupně nejvýše 2 s reálnými koeficienty (což je vektorový prostor dimense 3 nad tělesem reálných čísel)
a máme v něm dány polynomy

p(t)= t+2 , q(t)= t^2 - t , r(t)= t^2 - 2

(symbol x jsem si schoval pro jiný účel). O jejich lineární závislosti či nezávislosti rozhodne řešitelnost rovnice

(1) $x p(t) + y q(t) + z r(t) = 0$

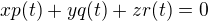
s neznámými x, y, z. Rovnice (1) při tom musí být splněna identicky (tj. pro každé reélné t). Připomeňme si, že polynom
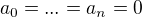$P(t) = a_0 t^0 + ... + a_n t^n$ je identicky roven 0, právě když $a_0 = ... = a_n = 0$ . Použitím této věty dostaneš pro neznámé x,y,z
soustavu třech rovnic, v níž se už nebude vyskytovat proměnná t.

vanok · 20. 10. 2011 15:24 — Editoval vanok (20. 10. 2011 15:28)

↑ jiskra:

no ale na prednaskach si bral poznamky a na wikipediu nie je nic???

Dobre tak ako sa pisu tie "vectory " v nasej baze 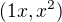$(1 x, x^2)$

Prvy ti napisem $p(x)= x+2 =2*1 + 1*x + 0* x^2$

To znamena ze v nasej baze ide o vektor (pisem ho ako vector slpec! dohoda co musis dodrzat v jednom cviceni)
$\left ( \begin{array}{ccc} 2 \\ 1 \\ 0\\ \end{array} \right )$

POKRACUJ A POZOR NA PORIADOK A AJ NULY SA PISU

Srdecne Vanok

jiskra · 20. 10. 2011 16:08

vanek: ty vektory se vzdy zapisuji jako sloupec? to jsem nevedel.

takze by vyslo? :
2 0 -2
1 -1 0
0 1 1

vanok · 20. 10. 2011 16:49

↑ jiskra:
Ano dobra odpoved na marticu lineairneho systemu
ALE vies napisat vsetki detaily ako si k tom prisiel?

Teraz aplikuj teoriu na matrici co si nasiel.

jiskra · 20. 10. 2011 20:13

takze postup:
q(x)= x^2 - x = 0.1 - 1x + 1x^2
q=[
0
-1
1]

r(x)= x^2 - 2 = -2.1 + 0x + 1^2
r=[
-2
0
1]

kdybyjsi mi nerekl , ze je mam zapsat do matice vertikalne, napsal bych je horizontalne a mel bych:
2 1 0
0 -1 1
-2 0 1

z matice
2 0 -2
1 -1 0
0 1 1
udelam:
1 0 -1
0 1 1
0 0 2

jiskra · 20. 10. 2011 20:54

jestli to teda nepletu tak:
_p____q_____r
1.x1 + 0.x2 - 1.x3 = 0
0.x1 + 1.x2 + 1. x3 = 0
0.x1 + 0.x2 + 2.x3 = 0
X1=X2=X3=0
a proto jsou polynomy p(x), q(x) a r(x) linearne nezavisle.

pokud by vyslo nekonecne mnoho reseni zavislych na parametru, taby by byly linearne zavisle. je to tak?

vanok · 20. 10. 2011 22:00

↑ jiskra:

Ano vysledok je dobry, aj na druhom riadku je jedno znamienko spatne
<<<
udelam:
1 0 -1
0 1 1
0 0 2>>>>>

a na prednaske ste videli ze ak na diagonale mas nenulove prvky a pod nou same nuly tak vectory z ktore si v matici upravoval su linearne nezavislt

Mala poznamka: aj z matricamy ked robis Gauss-ovu metodu je uzitosne pisat vssetki etapy a nic nerobit len v hlave

Srdecne Vanok

jiskra · 20. 10. 2011 22:24 — Editoval jiskra (20. 10. 2011 22:24)

z matice udelam:
2 0 -2 =1/2r1
1 -1 0 ~
0 1 1

1 0 -1
1 -1 0 = r2-r1
0 1 1 ~

1 0 -1
0 -1 1 ~
0 1 1 = r3+r2

1 0 -1
0 -1 1
0 0 2

to byla chyba pri opisovani :) (zena strasne otravovala)
hlavne ze ted do toho trochu vidim, nechtel jsem jen ukol opsat.

dekuji vanok i Rumburak, moc mi to podrobne vysvetleni pomohlo.

vanok · 20. 10. 2011 22:38

↑ jiskra:

Vyborne a poslednom riadku sa da este delit dvojkov

Dufam ze teraz budes aj sam vediet riesit take problemy

Srdecne Vanok

Matematické Fórum

#1 18. 10. 2011 11:33 — Editoval jiskra (18. 10. 2011 12:31)

Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#2 18. 10. 2011 11:46 Příspěvek uživatele ((:-)) byl skryt uživatelem jelena. Důvod: děkuji za upozornění, přesunuto

#3 18. 10. 2011 12:03 Příspěvek uživatele jiskra byl skryt uživatelem jelena. Důvod: děkuji za komentář - kopie v 1. příspěvku, přesun do VŠ

#4 18. 10. 2011 13:22

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

jiskra napsal(a):

#5 18. 10. 2011 13:53

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

vanok napsal(a):

jiskra napsal(a):

#6 18. 10. 2011 14:05 — Editoval Rumburak (18. 10. 2011 14:07)

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#7 20. 10. 2011 11:03

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#8 20. 10. 2011 11:18 — Editoval vanok (20. 10. 2011 11:52)

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#9 20. 10. 2011 11:27 — Editoval Rumburak (20. 10. 2011 11:45)

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#10 20. 10. 2011 11:54 — Editoval vanok (20. 10. 2011 11:54)

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#11 20. 10. 2011 12:22

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#12 20. 10. 2011 12:31

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#13 20. 10. 2011 13:33

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#14 20. 10. 2011 13:37 — Editoval vanok (20. 10. 2011 13:37)

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#15 20. 10. 2011 14:08

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#16 20. 10. 2011 14:12

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

Rumburak napsal(a):

#17 20. 10. 2011 15:21

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#18 20. 10. 2011 15:24 — Editoval vanok (20. 10. 2011 15:28)

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#19 20. 10. 2011 16:08

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#20 20. 10. 2011 16:49

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#21 20. 10. 2011 20:13

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#22 20. 10. 2011 20:54

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#23 20. 10. 2011 22:00

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#24 20. 10. 2011 22:24 — Editoval jiskra (20. 10. 2011 22:24)

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

#25 20. 10. 2011 22:38

Re: Vektorovy prostor P3={a0 + a1x + a2x^2...} a lin. zavisloti polynomu

Zápatí