Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 11. 2011 16:56
- night_gnome

- Příspěvky: 68
- Reputace: 0
limita funkce
Dobrý den, jak zjistit, zda má  limitu zprava v bodě 6, popř.: jakou?
limitu zprava v bodě 6, popř.: jakou?
Offline
- (téma jako vyřešené označil(a) night_gnome)
#2 21. 11. 2011 17:02
Re: limita funkce
Ahoj ↑ night_gnome:,
Nezda sa mi ze v 6 existuje limita.
Lebo sin tam velmi osciluje ....medzi -1 a 1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 21. 11. 2011 17:02 — Editoval Rumburak (21. 11. 2011 17:03)
Re: limita funkce
↑ night_gnome:
Zkus úlohu nejprve zjednodušit: prozkoumej otázku limity v 0 zprava pro funkci  .
.
Výsledek pak aplikuj na složitější funkci  .
.
Offline
#4 21. 11. 2011 17:05
- night_gnome

- Příspěvky: 68
- Reputace: 0
Re: limita funkce
↑ vanok:
limita neexistuje, jen nevím, jak to početně dokázat :/
Offline
#5 21. 11. 2011 17:11
Re: limita funkce
↑ night_gnome:
Vyjdi z tzv. Heineho definice limity a najdi dvě poslouonosti 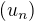 ,
, 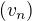 obě konvergující zprava k číslu 6 ale takové,
obě konvergující zprava k číslu 6 ale takové,
aby posloupnosti  ,
,  měly různé limity.
měly různé limity.
Offline
#6 21. 11. 2011 17:13 — Editoval vanok (21. 11. 2011 17:33)
Re: limita funkce
↑ night_gnome:,
Mozes pracovat ako navrhol kolega v okoli 0.
Pozri aj sem
http://www.math.washington.edu/~conroy/ … sin1overx/
A toto je zaujimava poznamka v tomto dokumente je
To see this, consider that sin(x) is equal to zero at every multiple of pi, and it wobbles between 0 and 1 or -1 between each multiple. Hence, sin(1/x) will be zero at every x = 1/(pi k), where k is a positive integer. In between each consecutive pair of these values, sin(1/x) wobbles from 0, to -1, to 1 and back to 0.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 21. 11. 2011 17:16 — Editoval night_gnome (21. 11. 2011 17:20)
- night_gnome

- Příspěvky: 68
- Reputace: 0
Re: limita funkce
↑ Rumburak:
bohužel, nevím jak řešit ani tu jednoduchou funkci  můžete mi to rozepsat ? Snad mě to nakopne a půjde mi to lépe...
můžete mi to rozepsat ? Snad mě to nakopne a půjde mi to lépe...
edit: rozumím tomu tak, že pokud zde již není žádná možnost jak se zbavit 0 ve jmenovateli -> limita nemá řešení ?
Offline
#8 21. 11. 2011 17:25
Re: limita funkce
↑ night_gnome:,
Skor, ak je viac hromadnych bodov v okoli bodu kde hladame limitu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 21. 11. 2011 21:22 — Editoval michaela20 (21. 11. 2011 22:30)
- michaela20

- Zelenáč
- Příspěvky: 8
- Reputace: 0
Re: limita funkce
Dobrý večer, nenašela by se dobrá, která si ví rady s těmito příklady?? Jsem v koncích..
lim (x> 0)=(sin4*x)/(sqrt(x+1)-1)
a
lim (x> 0-) = (sqrt(1-cos2*x)/x)
děkuji
Offline
#10 22. 11. 2011 00:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita funkce
↑ michaela20:
Zdravím, pokud potřebuješ více podrobně, založ si prosím, své vlastní téma (a příště vždy své vlastní), děkuji.
1) rozšířit výrazem 
2) použit vzorec pro 
Velmi užitečný materiál (děkuji autorům).
Offline
#11 22. 11. 2011 09:39 — Editoval Rumburak (22. 11. 2011 14:58)
Re: limita funkce
↑ night_gnome:
O.K. Řešme tedy nejprve otázku limity v 0+ funkce  . Funkce g je vlastně složenou funkcí tvaru
. Funkce g je vlastně složenou funkcí tvaru
 , kde
, kde  .
.
Pro  dostáváme, že
dostáváme, že  (snad je jasné, že tím míním výrok
(snad je jasné, že tím míním výrok  ).
).
Pokud by tedy existovata
(?)  ,
,
pak by podle věty o limitě složené funkce  muselo platit též
muselo platit též  .
.
Důkaz, že poslední limita neexistuje, zkusme proto opřít o skutečnost, že především neexistuje limita v (?) .
Bude výhodné postupovat sporem s Heineho definicí limity, tj. najděme dvě posloupnosti  ,
, 
jdoucí k  takové, aby existovaly limity
takové, aby existovaly limity
 ,
,  ,
,
které by však byly navzájem různé, tj.  . To bys mohla zvládnout. Až toto vyřešíš, bude Ti možná už zbytek jasný,
. To bys mohla zvládnout. Až toto vyřešíš, bude Ti možná už zbytek jasný,
kdyby ne, dej vědět.
Offline
#12 22. 11. 2011 10:34
- michaela20

- Zelenáč
- Příspěvky: 8
- Reputace: 0
Re: limita funkce
↑ jelena: Příště si založím vlastní téma. I to mi moc nepomohlo, nemohla bych poprosit o postup?
Offline
#13 22. 11. 2011 14:41
- night_gnome

- Příspěvky: 68
- Reputace: 0
Re: limita funkce
↑ Rumburak:
děkuji, už je mi to jasnější.
Offline
