Matematické Fórum

↑ elijah:Ahoj, návod by mohol byť aj tu

http://fyzikalniolympiada.cz/texty/odpor.pdf

↑ LukasM:
Rád se ti to pokusím objasnit, já tomu říkám různě ale správně by se mělo použít mezní rychlost, je to nejvyšší (konečná) reálnou rychlost pádu, kdy se gravitační síla vyrovná s odporovou silou prostředí (vzduchu) a dál už neroste. Pokud by tě to více zajímalo tak třeba zde: http://en.wikipedia.org/wiki/Terminal_velocity

Jo jinak s tou odporovou sílu u té vody, jsem právě myslel jestli by nešla zpočítat tak jak jsem uvedl: F=1/2*C*S*Ro*v^2 s tím že za Ro by se dosadila ne hustata vzduchu ale vody, teoreticky by to šlo, ale nevím.

↑ LukasM:
Tu Vm tam mam dodatečně , je pravda že tady je k ničemu mam to v tom excelu tak mi to počíta automaticky při zadaných hodnotách, takže to ted nerešme, puvodně je ta Vm určena pro vzduch, ale při zachování stejnych podmínek a dosazení hustoty vody místo vzduchu by to mělo být aspon tak zhruba. Ale jak ty říkáš je to konstatní síla.  Dozvěděl jsem se že ten vzorec: platí jen když je v objektu < v zvuku  takže bude výsledek nepřesný , nevím o kolik. Ten obsah jen jen tak hodil, protože nikdy nebude kvuli tvaru kůlky přesny musel by jsem to zjednodušit , že její boční profil odpovída obdelníku o délce a výšce projektilu. Což je 7,62x51=388,6 mm^2 = 0,0003886 m^2,  Doplnil jsem to tam a zachoval stejné podmínky jako nahoře, vyšlo mi že vychýlení bude: 0,134838246 m   což je sakramenský rozdíl :D  A ve vodě: 109,851 m


V té vodě to teda asi bude špatně, ale v tom vzduchu by to mělo být zhruba ok, nevím o žadném jiném vzorci pro odpor prostředí, který by byl vhodný pro supersonické rychlosti.

A při té vodě bych musel spočítat hodnotu té síly v každé sekundě jejího pohybu a sečíst všechny hodnoty,  potom bych dostal celkovou sílu.
Když nebudu brát v uvahu rychlost proudu vody pod jejím povrchem a budu brát, že je "klidná" a vím že ve vodě působí jak si psal  tíhová síla, vztlaková síla a síla odporová stále mi to nepomuže určit, v jaké hloubce by se její rychlost zpomalila skoro na nulovou a klesala volně na dno , a nebo za jaký čas by se dotkla dna.

spletl jsem si rychlost kulky s rychlostí bočního větru :D už sem z toho dost zblblej, tím padem by neměl být problém s rychlostí zvuku.

Plocha už je lepší, ale stejně je to moc. Není to ani přibližně . To druhé číslo je délka náboje, ne kulky. Viz třeba tenhle obrázek na wikipedii.

Jasně máš pravdu, bral jsem celou kulku, našel jsem obrázek přímo pro ten typ kůlky

Takže podle toho obrázku by měla čistá šířka projektilu být asi 70-50  = 20 mm a nová plocha by tedy byla 7,62mm*20mm = 152,4 mm^2 = 0,0001524 m^2 . Opět jsem to dosadil a vyšlo mi vychýlení 0,067686995 m  u té vody už to rači ani neřeším.

A ještě dotaz. Kde jsi vzal ten koeficient C? Ten musí taky odpovídat bočnímu profilu. (Jinak pokud vítr kulkou trochu pootočí, bude se měnit.)

Našel jsem jednu dobrou stránku kde se tím docela zabývají a mají tam grafy je to opravdu jen přibližná hodnota není urcite přesná, při té rychlosti kůlky by ji vítr neměl pootočit spiš jen posunout(ale co já vim).
Ta stránka je tu: http://www.balistika.cz/vnejsi_teorie.html   je tam i program kterej má počítat i s Coriolisova sílou ale já jsem ho moc nepobral. A ten graf z ktereho jsem vzal c je tady:

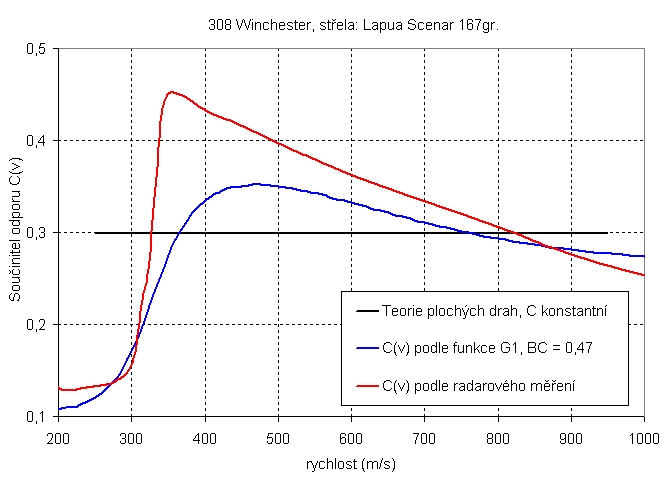
bral jsem to pro to c konstatní ty ostatní by měli být přesnější, ale vzal jsem to tak zhruba s tím že se to muže měnit v pruběhu dráhy jak píšeš.

o asi těžko. Musíš si ten čas rozkouskovat třeba po milisekundách, a v každém kroku spočítat aktuální sílu a vzdálenost, do které ta síla těleso posune během následující milisekundy. Stejně tak si budeš ukládat aktuální rychlost. Z té pak v dalším kroku spočítáš novou sílu, atd.

Pro přesnou hodnotu bych to musel udělat v ms jak pišeš , v excelu by to neměl být problém ale stejně nevím jestli by se ten výsledek alespon trochu blížil realitě.

Pokud jde o tu vodu, nějak jsi změnil zadání, a já nevím co vlastně řešíš.

Ta voda mě štve už dlouho. Řeším přesně ty 2 typy co jsem napsal, a nikdo mi není schopen to vysvětlit nebo objasnit , jak by to šlo spočítat. Možná jsem to napsal debilně ale nevím jak jinak to mám vysvětlit. Vezmu to konkrétně.

1) Skočím z utesu který má 20 m do vody, a chci spočítat jak hluboko se potopím než mě kyslík v plicích začně unášet na hladinu.

2) Když vhodím kovovou kuličku do jezera které je hluboké X metrů za jaký čas se kulička dotkne dna.
(když budu brát že ve vodě nebudou žadné unášivé proudy)

Celé je to ale spíš hraní, se skutečným světem to asi nebude mít moc společného. Hodně bych se divil kdyby takhle složitý problém šel popsat takhle triviálním vzorcem.

Stačila by mi hrubá hodnota, která by se alespon trochu bližila realitě, s tím bych se spokojil. Vycházim z podobné témy která se už tady řešila http://forum.matweb.cz/viewtopic.php?id=30058 nevím z kama uživatel o.neill vzal ten vzorec na to vychýlení ale jelikož je to vyřešené předpokladám, že by měl byt správně.

Jinak děkuji za pomoc, jsem rád že se se mnou alespon někdo baví. Je třeba škoda, že se tu nevyjádřil uživatel Pavel Brožek  věřím že ten by to dokázal říct co je nesmysl a co by šlo.

↑ LukasM:

1) to samé v bledě modrém. Pokud věříš tomu vzorci, výpočet si udělej v Excelu. Já bych ale vzorci určitě nevěřil. Navíc koeficient C zase nikde nenajdeš a budeš si ho muset vymyslet, takže bych se tím nezabýval.

No já z toho vzorce umím spočítat vychílení nebo odporovou sílu prostředí, ale nevím přesně jaký vzorec bych měl použít abych spočítal tu hloubku potopení.

2) to je už zajímavější. I tady pomůže Excel, a tentokrát už výsledky možná k něčemu budou. Pro malé rychlosti navíc platí Stokesův vzorec, takže podle konkrétních parametrů by se dal možná použít. Ten popisuje právě ten prípad, kdy je síla úměrná jen první mocnině rychlosti, ne druhé. Potřebné najdeš tady. Podobnou úlohu jsme dělali v praktikách, podívej se sem na úlohu 6 (vnitřní třetí), něco na tom opravdu je. Můžu ti poslat svůj protokol z toho měření, kdyby tě to zajímalo.

Na ten protokol bych se rád podíval pokud mi jej mužeš poslat budu jen rád.

To asi těžko. Musíš si ten čas rozkouskovat třeba po milisekundách, a v každém kroku spočítat aktuální sílu a vzdálenost, do které ta síla těleso posune během následující milisekundy. Stejně tak si budeš ukládat aktuální rychlost. Z té pak v dalším kroku spočítáš novou sílu, atd.

Tohle bych chtěl zkusit, ale nejsem si jistý jestli to dobře chápu. Když to vezmu pro ten vzduch tak musím počítat v každé milisekundě odporovou sílu a to vychýlení ?  dále mam pak počítat aktualní rychlost v každé milisekundě dle vzorce v=a*t ? a všechny ty síly pak sečtu a dosadím do toho vzorce? Potřeboval bych to trochu více rozepsat abych vědel konkretně co mám udělat, pak bych to zkusil.

V tom vzduchu je to ok za předpokladu, že si můžeš dovolit počítat s konstantní boční silou. Ve skutečnosti to úplně tak není, protože, jak jsem už psal, jakmile ta síla začne působit, bude kulku urychlovat do boku, a tím pádem se ta síla bude během letu snižovat (závisí dokonce na čtverci rychlosti, takže to tam nějakou nepřesnost vnese). Jakou zhruba, to si můžeš zkusit v Excelu,

Podle čeho tady zjistím o kolik se bude ta síla snižovat ? Mužes mi prosím objasnit ten čtverec rychlosti? Nějak mě asi minul.

Díky

pošli mi to na freem@seznam.cz díky.

No já z toho vzorce umím spočítat vychílení nebo odporovou sílu prostředí, ale nevím přesně jaký vzorec bych měl použít abych spočítal tu hloubku potopení.

Neumíš, protože neznáš C. A i když si ho vymyslíš, tak ti to asi nepůjde, protože odporová síla závisí na rychlosti, jak tady už posté píšu, a tedy bez nějaké znalosti řešení diferenciálních rovnic to asi nepůjde. Proto tě pořád odkazuju na Excel, kde si to můžeš rozkouskovat a tomu řešení se tak vyhnout.

Problém je v tom že nemám ponětí jak to v tom excelu spočítat, neznám takové vzorce a musel bych si to hodne promyslet abych to mohl uskutečnit.

Jak to udělat jsem tam napsal. V každém kroku spočítat sílu, ze které snadno získáš zrychlení, a když máš zrychlení tak víš, o kolik se změnila rychlost tělesa za tu 1ms. Žádné síly sčítat nebudeš, to jsem už taky psal. Celou dobu si průbežně počítáš "vychýlení" (jak sám píšeš), takže se stačí podívat jaké je to vychýlení na konci.

Toto zkusím udělat a výsledek tu pak hodím, jen pro informaci jestli je to správně.