Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 20. 09. 2008 17:53 — Editoval lukaszh (20. 09. 2008 17:55)
Re: Lineární lomená funkce
↑ budak:
Záleží od toho, čo myslíš pod "robi? funkciu" :-) Ak myslíš priebeh funkcie, tak treba urči? definičný obor a obor hodnôt. Ďalej extrémy, kde pre "podozrivé" body na extrémy platí  . Keďže grafom danej lomenej funkcie je hyperbola treba urči? asymptoty
. Keďže grafom danej lomenej funkcie je hyperbola treba urči? asymptoty  , kde
, kde  a
a  . Potom zistíš, či je funkcia sudá, lichá, prostá, periodická, neperiodická atd... Skrátka, postupuješ podľa pravidiel pri určovaní priebehu funkcie.
. Potom zistíš, či je funkcia sudá, lichá, prostá, periodická, neperiodická atd... Skrátka, postupuješ podľa pravidiel pri určovaní priebehu funkcie.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#4 20. 09. 2008 19:23
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Lineární lomená funkce
↑ budak:
Pokud máme lineární lomenou funkci  , kde
, kde  a
a  (aby to bylo vůbec zajímavé), pak můžeme upravovat:
(aby to bylo vůbec zajímavé), pak můžeme upravovat:
Z tohoto výrazu je zřejmé, že graf funkce f získáme posunutím grafu funkce  o
o  ve směru kladné osy x, poté přenásobením číslem
ve směru kladné osy x, poté přenásobením číslem  (pokud je toto číslo záporné, pak se graf "převrátí" podle osy x) a nakonec posunutím o
(pokud je toto číslo záporné, pak se graf "převrátí" podle osy x) a nakonec posunutím o  ve směru kladné osy y.
ve směru kladné osy y.
Je také zřejmé, že  . Protože čitatel zlomku
. Protože čitatel zlomku  je nenulový, tak funkce nikdy nenabývá hodnoty
je nenulový, tak funkce nikdy nenabývá hodnoty  . Obor hodnot funkce tedy bude
. Obor hodnot funkce tedy bude  .
.
Toto nejsou věci, které by sis musel pamatovat, stačí jen vědět jak lineární lomenou funkci upravovat, abychom ji dostali do tvaru, z kterého jsou tyto věci zřejmé. Zkus upravit tu tvoji funkci, jestli se ti to nepodaří, můžu ten postup rozepsat konkrétně pro ni.
Offline
#5 20. 09. 2008 20:06
Re: Lineární lomená funkce
↑ budak:
lukaszh ti pise dobre.. ak vies kde je funkcia parna, neparna, periodicka, kde ma inflexne body, kde je konkavna konvexna, aky je jej definicny obor, obor hodnot .... atd. tak na zaklade toho vies zostrojit pomerne presny graf danej funkcie :) ono nie vzdy je to lahke nakreslit ten graf..ako napr  .. to uz robis z hlavy.. ak ti neni nieco jasne treba to dostudovat
.. to uz robis z hlavy.. ak ti neni nieco jasne treba to dostudovat
Offline
#6 20. 09. 2008 23:58
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Lineární lomená funkce
Misto pouzivani a, b, c,d jako Brozek (coz je samozrejme spravne) na to jdu jinak. Nezarucuji, ze to je 100 % spolehlive.
Napred si urcim Df. Ze jmenovatele urcis, ktera hodnota tam nepatri a tuto nemuzes na X pouzit. Tim padem tam se "posune" osa y, protoze to dane x neni v Df.
Co se tyce y, tak je to to podobny posun. Ale o kolik? Jednoduse spocitame "limitu" dane funkce. Zde nam vychazi 2, takze dvojky to nenabyde, takze do te se posune osa x.
Pocitam to takhle, kdyz si nevzpomenu na nic jineho.
Offline
#9 21. 09. 2008 11:49
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Lineární lomená funkce
↑ budak:
Nebo tím postupem co jsem uvedl já:
Je to tedy funkce  posunutá o 3 "doprava", přenásobená číslem 7 a posunutá o 2 "nahoru". Nejdříve sestrojíš asymptoty a poté je asi vhodné zvolit si dva body (jeden nalevo a druhý napravo od svislé asymptoty), pro které spočteš funkční hodnotu. Graf vypadá takto (červeně jsou vyznačené asymptoty):
posunutá o 3 "doprava", přenásobená číslem 7 a posunutá o 2 "nahoru". Nejdříve sestrojíš asymptoty a poté je asi vhodné zvolit si dva body (jeden nalevo a druhý napravo od svislé asymptoty), pro které spočteš funkční hodnotu. Graf vypadá takto (červeně jsou vyznačené asymptoty):
Offline
#10 17. 05. 2012 13:52 — Editoval Magicmaster (17. 05. 2012 13:56)
- Magicmaster

- Místo: Plzeň
- Příspěvky: 47
- Škola: FIT ČVUT
- Pozice: Student
- Reputace: 1
Re: Lineární lomená funkce
↑ halogan:
[s]Mohl byste objasnit, co myslíte tou "limitou" funkce? Limita této fce neexistuje a jednostranné jsou 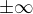 [/s]
[/s]
Edit: Už jsem si to uvědomil. Limitu je třeba udělat pro x jdoucí k nekonečnu. Pardon
Offline

