Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vzájemná poloha přímky a kružnice (TOTO TÉMA JE VYŘEŠENÉ)
#2 15. 01. 2012 08:07
Re: Vzájemná poloha přímky a kružnice
↑ Lukas 22:
Přímky  nebo kružnice
nebo kružnice  ?
?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 15. 01. 2012 08:13
#4 15. 01. 2012 09:12
Re: Vzájemná poloha přímky a kružnice
↑ Lukas 22:
rovnice kružnice má tvar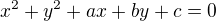
postupně dosadíš souřadnice bodů do této rovnice
a vyřešíš tuto soustavu. Asi nejjednodušší je odečíst (2)-(1) a pak (2)-(3) a tím se zbavit 

a vyřešit tuto soustavu už by neměl být problém.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 15. 01. 2012 09:19
#6 15. 01. 2012 09:37
Re: Vzájemná poloha přímky a kružnice
↑ zdenek1:
prosimtě napsal bys mi tu tu konečnou rovnici abych věděl že jsem to vypočítal správně?? dík
Offline
#7 15. 01. 2012 10:48
#9 15. 01. 2012 11:13
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Vzájemná poloha přímky a kružnice
↑ Lukas 22:
Máš tyto 2 rovnice od Zdenka

Dopočteme c z rovnice:
A teď koeficienty a,b,c dosadíme do rovnice: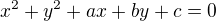 dostaneme:
dostaneme:
Rovnice kružnice:
Nikdo není dokonalý
Offline
#10 15. 01. 2012 11:19
Re: Vzájemná poloha přímky a kružnice
Jinak ještě jen dodám další možnost, jak úlohu řešit, třeba se ti bude líbit víc( byť je asi delší, ale procvičíš se při tom a uvědomíš si pár věcí :) )
Ty tři body ti tvoří trojúhelník a kružnice je tomu trojúhelníku opsaná. Střed os stran tvoří střed kružnice, takže stačí zjistit průsečík dvou os stran.
Baf!
Offline
#13 15. 01. 2012 14:35
Re: Vzájemná poloha přímky a kružnice
↑ Lukas 22:
poloměr = vzdálenost SA
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#14 15. 01. 2012 14:42 — Editoval Chuck Brown (16. 01. 2012 14:53)
- Chuck Brown
- Zablokovaný
- Příspěvky: 2
- Reputace: 0
Re: Vzájemná poloha přímky a kružnice
It is an excellent post.
It is also very interesting.
alcohol tester
Offline
#15 15. 01. 2012 14:44
Re: Vzájemná poloha přímky a kružnice
↑ zdenek1:
a když vypočítám tu vzdálenost tak kam to dosadím ??
Offline
#16 15. 01. 2012 14:45
Re: Vzájemná poloha přímky a kružnice
↑ Lukas 22:
do obecké rovnice kružnice Odkaz
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#18 15. 01. 2012 14:50
Re: Vzájemná poloha přímky a kružnice
↑ Lukas 22:
ano, to je poloměr
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#19 15. 01. 2012 14:56
Re: Vzájemná poloha přímky a kružnice
↑ zdenek1:
tak konečný výsledek bude: 
jak jsem tam dosadil ten bod 3 a 5 tak to je vlastně ten bod S[-3;5] ??
Offline
#20 15. 01. 2012 15:01
Re: Vzájemná poloha přímky a kružnice
↑ Lukas 22:
Ano.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#21 31. 01. 2012 15:43
Re: Vzájemná poloha přímky a kružnice
↑ zdenek1:
Prosimtě neporadil by jsi mi s tímto příkladem??
Napište rovnici kružnice, která prochází bodem M![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) a která se dotýká osy x v bodě T
a která se dotýká osy x v bodě T![kopírovat do textarea $[3,0]$](/mathtex/9b/9bacc6f39c3a103bbbff4f24da977cd8.gif)
Offline
#23 31. 01. 2012 16:30 — Editoval Cheop (31. 01. 2012 17:33)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Vzájemná poloha přímky a kružnice
↑ Lukas 22:
Obecná rovnice kružnice se středem S=(m; n) a poloměrem r má rovnici: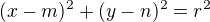
Ty máš 2 body, kterými ta kružnice prochází
2 rovnice budou:
Třetí rovnice bude  a to proto, že se hledaná kružnice má dotýkat osy x
a to proto, že se hledaná kružnice má dotýkat osy x
Máš tedy 3 rovnice o 3 neznámých.
Stroj to řeší (ty si to cvičně udělej na papír)
Mělo by ti vyjít:
Nikdo není dokonalý
Offline
#24 31. 01. 2012 16:31
- Chuck Brown
- Zablokovaný
- Příspěvky: 2
- Reputace: 0
Re: Vzájemná poloha přímky a kružnice
I think the post is great but i can not understand this language. please tell me about it.
Offline
#25 01. 02. 2012 00:52
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzájemná poloha přímky a kružnice
↑ Chuck Brown:
It is about problem "find the Equation of a Circle (given three points A[5;1] B[0;6] C[4;-2])". OK?
Cheers
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Vzájemná poloha přímky a kružnice (TOTO TÉMA JE VYŘEŠENÉ)


