Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 10. 10. 2008 01:03
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Jevy závislé
Na tomhle fóru mě fascinují sebevědomé volby přezdívek. Krom Slabeho_matematika,antitalenta,lamy,hlupuckeho,blbce,blbouna už tu máme i blba...
Jevy A a B jsou nezávislé, pokud pravděpodobnost, že nastane druhý, pokud nastal první, je stejná, jako pravděpodobnost, že nastane druhý.
Příklad: pravděpodobnost, že na kostce padne šestka je 1/6. Pravděpodobnost, že na minci padne orel je 1/2. Ta druhá pravděpodobnost je 1/2 i za předpokladu, že na kostce padla šestka. Proto jsou jevy na sobě nezáislé. To odpovídá i intuitivnímu pojetí -- výsledek hodu kostkou nezáleží na výsledku hodu mincí a naopak, hody jsou nezávislé.
K našemu příkladu. Pravděpodobnost, že padne sudé číslo je 1/2 (počet příznivých jevů je 3 -- padla 2,4 nebo 6, počet všech 6 --padla 1,2,3,4,5 nebo 6, pravděpodobnost 3/6=1/2). Pravděpodobnost, že padne sudé číslo za předpokladu, že padla pětka nebo šestka je opět 1/2 (počet příznivých jevů je 1 -- padla šestka, počet všech 2 -- padla pětka nebo šestka, pravděpodobnost 1/2)
Pravděpodobnosti jsou v obou případech stejné, jevy jsou proto nezávislé.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 10. 10. 2008 08:07 — Editoval musixx (10. 10. 2008 08:51)
Re: Jevy závislé
↑ Kondr: Zdravim! Ve stylu Tveho argumentu: pravdepodobnost, ze padne petka nebo sestka je 1/3. Za predpokladu, ze padla petka nebo sestka, je pravdepodobnost 1/2, ze padlo sude cislo (musela to byt sestka). Naopak: Pravdepodobnost, ze padne sude cislo je 1/2. Za predpokladu, ze padlo sude cislo, je pravdepodobnost, ze padla petka nebo sestka (vlastne je to redukovano jen na sestku) opet 1/3.
S Tvou interpretaci jevu zavislych a nezavislych bych souhlasil, ale rekl bych, ze musime uvazit obe strany: Tedy navic i to, ze jako prvni bude jev "druhy" a jako druhy bude jev prvni. Zadne explicitni setrizeni jevu preci na zacatku nemame...
EDIT:
Beru zpet mou namitku. Musel jsem si to jen vic rozmyslet. Necht pro jev A s p(A)=a a jev B s p(B)=b plati p(A|B)=a. Pak uz nutne
(treti rovnost plati, protoze jsme predpokladali, ze 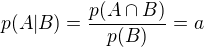 ).
).
Offline