Matematické Fórum

cs.pata

Čaute ,nerozumím jednomu kroku u řešeného příkladu v učebnici a prosím někoho jestli by mi ho vysvětlil :)
Zadání:(tady tomu všemu ještě rozumim) $\int_{}^{}\frac{2x+3}{(4x^{2}-4x+3)^{2}}dx=\frac{1}{4}\int_{}^{}\frac{8x-4}{(4x^{2}-4x+3)^{2}}dx+4\int_{}^{}\frac{1}{((2x-1)^{2}+2)^{2}}dx=\frac{1}{4}I_{1}+4I_{2}$
$I_{2}=\int_{}^{}\frac{1}{((2x-1)^{2}+2)^{2}}dx=|t=2x-1,dt=2dx|=\frac{1}{2}\int_{}^{}\frac{1}{(t^{2}+2)^{2}}dt=\frac{1}{2}(\frac{t}{4(t^{2}+2)}+\frac{1}{4}\int_{}^{}\frac{1}{t^{2}+2}dt)=$
$=\frac{1}{8}(\frac{t}{t^{2}+2}+\frac{1}{\sqrt{2}}arctg\frac{t}{\sqrt{2}})+c$
tady u řešení I2 chápu tu substituci ale nerozumím jakým zpusobem vznikl najednou v te první závorce dva zlomky:( prosím o radu

Alivendes

Chvilku strpení, uvedu srozumitelnější postup:

$\int \frac{2x+3}{(4x^2-4x+3)^2}dx$
$\int \frac{2x+3}{[(2x-1)^2+2]^2}dx$

$2x-1=t$
$2dx=dt$
$dx=\frac{dt}{2}$
$2x+3=t+4$

$\frac{1}{2}\int \frac{t+4}{(t^2+2)^2}dt=\frac{1}{2}\int \frac{1}{t^2+2}dt+\int \frac{1}{(t^2+2)^2}dt$

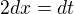
Ten druhý integrál by měl jít přes substituci $t^2+2=u$ a pak znovu přes parciální zlomky.

To co je nahoře mi přijde dost nepřehledné.

cs.pata · 04. 03. 2012 13:18

↑ Alivendes:ja jako rozumím tomu začatku kdy se převede ten zlomek na derivaci jmenovatele do čitatele a rozděli se to pak na dva zlomky a ja pak právě nerozumim tomu postupu u I2 což je ten $I_{2}=\int_{}^{}\frac{1}{((2x-1)^{2}+2)^{2}}dx$ myslíš jako že je to rozklad na parcialní zlomky ?

jelena · 05. 03. 2012 23:28

↑ cs.pata:

Zdravím,

řekla bych, že po substituci 2x-1=t pro integrál $\frac{1}{2}\int_{}^{}\frac{1}{(t^{2}+2)^{2}}\d t$ je použita metoda Ostrogradskogo (neurčitých koeficientů) - brali jste? Odkud je toto řešení?

Metodu umí MAW, teď jsem zkoušela zadávat a nenapsal, že používá Ostrogradského, zklamání :-)

Podařilo se dojit k výsledku? Děkuji.

cs.pata · 06. 03. 2012 08:08

↑ jelena:ahoj,
ne tu metodu neznam, zkoušel jsem ruzne metody,per partes, další substituci i rozklad na parcialní zlomky ale nic z toho nevyšlo těch $\frac{1}{2}\int_{}^{}(\frac{t}{4(t^{2}+2)}+\frac{1}{4}\int_{ }^{}\frac{1}{t^{2}+2})dt$ toto řešení je ze skript z naši fakulty

jelena · 06. 03. 2012 12:19

↑ cs.pata:

Měl by fungovat i rozklad na parciální zlomky, ovšem jelikož kořen je komplexní, tak v čitatelích má být (Ax+B), (Cx+D).

Metody (Ostrogradskogo) jsou například zde (str. 16 pdf) nebo zde.

Jinak teď máš překlep v zápisu, u 1. zlomku nemá být integrál.

$\frac{1}{2}\int_{}^{}\frac{1}{(t^{2}+2)^{2}}\d t=\frac{1}{2}$\frac{t}{4(t^{2}+2)}+\frac{1}{4}\int_{ }^{}\frac{1}{t^{2}+2}dt$$ .

Zkus to rozepsat, pokud máš zájem o kontrolu. Že nevyšlo, to je slabá informace (stejně, jako "naše fakulta" :-)

kaja.marik · 06. 03. 2012 12:48

Mozna se tam pouzil rekurentni vzorec - neco jako http://www.math.muni.cz/~xschlesi/bakal … tml#pr:for

Metodu umí MAW, teď jsem zkoušela zadávat a nenapsal, že používá Ostrogradského, zklamání :-)

Pekny den, Ostrogradski mel tech metod hodne. V MAWu bereme jako ostrogradskeho metodu tu metodu, ktera ma ve jmenovateli integrovane funkce odmocninu z kvadratickeho vyrazu. Asi bych to pojmenovani mel zmenit, ale co chudaci prekladatele .. :)

kaja.marik · 06. 03. 2012 12:50

Alivendes napsal(a):
Ten druhý integrál by měl jít přes substituci $t^2+2=u$ a pak znovu přes parciální zlomky.

Tpo nepujde, vznikne tam odmocnina. Je to parcialni zlomek, tak bych pouzil postup predepsany pro tento typ parcialnich zlomku.

cs.pata · 06. 03. 2012 15:12

↑ jelena:ahoj tu metodu rozkladu na parcialní zlomky jsem už zkoušel a vycházeli 0,0,0,1 a podle http://calc101.com je to to samé :( a není to typ příkladu kde se přidá nějaké realne číslo aby vznikl vzorec?

jelena · 06. 03. 2012 16:37

Zdravím v tématu

↑ kaja.marik:

:-) polovina překladatelského týmu oznámila, že do konce dubna nemá čas, ovšem druhá polovina je odhodlana provádět opravy. Při této přiležitosti jsme zjistili, že východní Vedoucí projektu již neučí na VŠ, ale je v bance, plně se věnuje ekonometrice (ale našel čas a udělil mi povolení umístit přilepená témata do příslušných sekcí).

↑ cs.pata:

mně vyšel takový výsledek (jak máš), když jsem použila metodu Ostrogradskogo, jak znám a jak je v odkazu. Nebo použiješ rekurentní vzorec, jak doporučuje vážený kolega ↑ kaja.marik:.

Zde je odvození s přičtením- odečtením (příklad 6.55). Bohužel, mám nějaký problém s počítačem, tak to je všechno, co teď napíši. Ať se podaří.

cs.pata · 06. 03. 2012 17:15

↑ jelena:už vyšlo :) použil jsem tu metodu Ostrogradskogo a mam to z krku :) diky moc

Alivendes · 06. 03. 2012 19:32

↑ kaja.marik:

Vidím, nakonec to dobře dopadlo :-)

jelena · 07. 03. 2012 23:53

↑ cs.pata:

děkuji za zprávu, jen pro pořádek - dle českého pravopisu (byla jsem poučena :-) máme v těchto případech psát Ostrogradského.

↑ kaja.marik:

to měl :-) Ale jelikož zde považuji použití s odmocninou za naprosto v pořádku a nepřekvapuje to, tak zřejmě metodou Ostrograského rozumím každou variantu, kdy se vyčlení zlomek, koeficienty a levá a pravá strana se derivuje.

Pohodu přeji.

Matematické Fórum

#1 04. 03. 2012 11:43 — Editoval cs.pata (04. 03. 2012 11:44)

Integrace racionální funkce

#2 04. 03. 2012 12:19 — Editoval Alivendes (04. 03. 2012 12:31)

Re: Integrace racionální funkce

#3 04. 03. 2012 13:18

Re: Integrace racionální funkce

#4 05. 03. 2012 23:28

Re: Integrace racionální funkce

#5 06. 03. 2012 08:08

Re: Integrace racionální funkce

#6 06. 03. 2012 12:19

Re: Integrace racionální funkce

#7 06. 03. 2012 12:48

Re: Integrace racionální funkce

#8 06. 03. 2012 12:50

Re: Integrace racionální funkce

Alivendes napsal(a):

#9 06. 03. 2012 15:12

Re: Integrace racionální funkce

#10 06. 03. 2012 16:37

Re: Integrace racionální funkce

#11 06. 03. 2012 17:15

Re: Integrace racionální funkce

#12 06. 03. 2012 19:32

Re: Integrace racionální funkce

#13 07. 03. 2012 23:53

Re: Integrace racionální funkce

Zápatí