Matematické Fórum

bons · 20. 10. 2008 10:50

ja vim že to jsem mozna nepatří, ale tohle mi počítáme

1. Regenerace rozpouštědla je prováděna v rektifikační kolone, nastřík do kolony dosahuje 12% hmotnosti Alkoholu a je přiváděn v množství 300kg/h. Destilát obsahuje 75% hm. alkoholu, destilační zbytek 0,5% alkoholu. Kolik bude destilátu a destil. zbytku do hodiny.

2. V 1 m3 (krychlovim) plynu je obsaženo 200g N (dusíku) (M=28g/mol) jeho tlak je 9atmosfér. teplota 20°c (R= 0,082) Vypočítejte počet molů dusíku a jeho parciální tlak.

Stimahle dvouma typama si nevim rady:(

jelena · 20. 10. 2008 13:02 — Editoval jelena (21. 10. 2008 23:15)

↑ bons:

Zdravím :-)

násobit, dělit budeme - tedy patří :-)

Zadání 1.

Je potřeba sestavit materialovou bilanci procesu (zákon zachování hmoty platí)

m = 300 kg (hmotnost původního rozpouštědla), w = 12 % (obsah alkoholu v původním rozpoštědle),
m_d=x (hmotnost destilátu), w_d = 75 % (obsah alkoholu v destilátu)
m_z = 300-x (hmotnost zbytku), w_z = 0,5 % (obsah alkoholu ve zbytku)

m * w = m_d * w_d + m_z * w_z

300 * 12 = x * 75 + (300 - x) * 0,5

Zadání 2.

Je potřeba použit Daltonův zákon a vzorec na parciální tlak plynu: třeba zde na str. 56 http://www.studopory.vsb.cz/studijnimat … Chemie.pdf

Jednotky už jsou zadány tak, že univerzální plynova konstanta R je upravena pro tlak v atm (kontrolováno zde: http://www.energetik.cz/hlavni3.html?m1 … tanta.html ) To znamená, že i vysledek parc. tlaku bude v atm (pokud je potřeba, budeš muset převádět do SI)

V směsí = 1 m^3

T - převest do Kelvin (20 + 273)

počet molů dusíku n_1 = m/M_r = 200/28

Celkový tlak plynu snad ani není potřeba, ale je možne, že je zadan kvuli tomu, že je tak velky, že místo zákonů pro ideální plyn použijeme van der Waalsovu rovnici pro reální plyn (v textu, na ktery se odkazuji, je o str. dál). V tomto případě pro dusík platí a= 0,135, b=38,6 . 10^(-6).

OK?
-----

Adam · 20. 10. 2008 17:38

Ahoj, potřeboval bych od Vás prosím pomoct s úlohou, která se jeví jednoduše, ale mně se přijde dost zapeklitá=)

Plníme rybník dvěma vpustěma. Pokud jej plníme oběma najednou, je naplněn za 6min, pokud jen vpustí A trvá to o pět minut déle než jen vpustí B.

kaja.marik

↑ Adam:
Počítat se má počet kaprů? Objem rybníka? Průtok vpustí B? Nebo za jak dlouho se naplní vpustí A?

jelena · 20. 10. 2008 18:28 — Editoval jelena (20. 10. 2008 18:30)

↑ Adam:

Zdravím :-)

Síce neuvádíš, co se má hledat, ale ukážu, jak se dostaneme třeba na rychlosti plnění :-)

Budeme předpokladat, že plníme reakční nádrž o neznamém objemu (když už jsme na VŠ tématech :-).

x - rychlost plnění přes 1. vpus?
y - rýchlost plnění přes druhou vpust.

plníme najednou za 6 minut, můžeme vypočítat objem nádrže: V=6(x+y)

Jak dlouho bud trvat naplnění pouze vpusti A? (čas plnění = objem / rychlost plnění), tedy

t_1 = V/x = 6(x+y)/x

Jak dlouho bud trvat naplnění pouze vpusti B?

t_2 = V/y = 6(x+y)/y

Víme, že doba plnění přes A je o 5 minut delší, než doba plnění přes B

t_1 - t_2 = 5

$\frac{6x+6y}{x} - \frac{6x+6y}{y} = 5$

$6 +\frac{6y}{x} - 6 -\frac{6x}{y} = 5$

$\frac{6y}{x} -\frac{6x}{y} = 5$ označím x/y = a

$\frac{6}{a} -6a = 5$

$-6a^2-5a+6 = 0$

$6a^2+5a-6 = 0$

a_1, 2 = -18/12 nebo 2/3

Zápornou hodnotu nebereme (to bychom museli jednu vpust přeměnit na výpust), z toho plyne x/y = 2/3.

Můžeme zvolit první možnost x = 2, y = 3 (také násobky těchto hodnot)

Co s tim podnikneš dál, už nevím, ale hodně zdaru :-)

bons · 21. 10. 2008 16:42 — Editoval bons (21. 10. 2008 16:43)

↑ jelena:
m = 300 kg (hmotnost původního rozpouštědla), w = 12 % (obsah alkoholu v původním rozpoštědle),
m_d=x (hmotnost destilátu), w_d = 75 % (obsah alkoholu v destilátu)
m_z = 300-x (hmotnost zbytku), w_z = 0,5 % (obsah alkoholu ve zbytku)

m * w = m_d * w_d + m_z * w_z

300 * 75 = x * 12 + (300 - x) * 0,005

jenom jeden dotaz, podle vzorecku, ktyrý ste mi napsala, nemelo by to být 300*0,12=x*0,75+(300-x)*0,5 ?? PS: jde o procenta tak nevim spis si mylsim ze by to melo bejt takhle:)

bons · 21. 10. 2008 16:52

Ješte jedna uloha,kterou jsem pocital:)
Je třeba připravit 500 kg rozkoku H2SO4 o koncentraci 40% k dispozici jsou dva rotoky 90 % a 30% H2SO4. Jáke množství těchto kyselin je třeba použít?
počítal jsem to takhle
m1=x
m1=500*0,4/0,9
m1=222,22
ze vztahu m1+m2=m3
takže m2=500-222,22
pozn. to m1 jsem pocital s tim 90% roztokem H2S04

jelena · 21. 10. 2008 23:35

↑ bons:

Zdravím :-)

určitě to mělo být přehozeno (12, 75), omlouvám se za překlep:

300 * 12 = x * 75 + (300 - x) * 0,5 (0,5 mám zapsano dobře)

Co se tyče jednotek - pokud všude dám procenta, tak je to v poradku.

Pokud mám v planu dávat hmotnístní zlomky, pak místo % zapiší číslo 100 krat menší (tedy ne 75 %, ale 0,75 apod.) Ale nemá to žádný význam, všude bych nechala procenta.

Pojem "hmotnostní procenta", což je "kolik kg složky na kg směsí", vyjádřeno v %. Slovo hmotnostní má význám pouze ve smyslu, abychom odlišili třeba procenta objemová (např. ml složky na ml směsi) - což se může užívat u kapalných latek, ale má spíše okrajový význam.

---------------
Zadání "Kyselina":

Je třeba připravit 500 kg roztoku H2SO4 o koncentraci 40% k dispozici jsou dva roztoky 90 % a 30% H2SO4. Jáke množství těchto kyselin je třeba použít?

Úplně stejný postup:

m = 500 kg (nového roztoku), w = 40 %,
m_1=x (hmotnost "husté" kyseliny), w_1 = 90 %
m_2 = 500-x (hmotnost slabší kyseliny), w_2 = 30 %

m * w = m_1 * w_1 + m_2 * w_2

500 * 40 = x * 90 + (500 - x) * 30

---------------------------------------------------

Pravidelně na tomto foru dávám odkaz na můj příspěvek číslo 38 o směsích: http://forum.matweb.cz/viewtopic.php?id=55&p=2

A? poslouží :-)

bons · 22. 10. 2008 08:52

Je potřeba použit Daltonův zákon a vzorec na parciální tlak plynu: třeba zde na str. 56 http://www.studopory.vsb.cz/studijnimat … Chemie.pdf

Jednotky už jsou zadány tak, že univerzální plynova konstanta R je upravena pro tlak v atm (kontrolováno zde: http://www.energetik.cz/hlavni3.html?m1 … tanta.html ) To znamená, že i vysledek parc. tlaku bude v atm (pokud je potřeba, budeš muset převádět do SI)

V směsí = 1 m^3

T - převest do Kelvin (20 + 273)

počet molů dusíku n_1 = m/M_r = 200/28

Celkový tlak plynu snad ani není potřeba, ale je možne, že je zadan kvuli tomu, že je tak velky, že místo zákonů pro ideální plyn použijeme van der Waalsovu rovnici pro reální plyn (v textu, na ktery se odkazuji, je o str. dál). V tomto případě pro dusík platí a= 0,135, b=38,6 . 10^(-6).

takže abych to pochopil tohle tak budu pouzivat tenhle vzorec p_a=(n_a*R*T)/V_s
takže P_a=(7,14*0,082*293)/1 (takhle by to melo byt že?:) )
molarní hmotnost mi vyslo 7,14

bons · 22. 10. 2008 09:36

Tak mam tu jeste jeden divnej příklad..podle Jeleny zpusoby mi to nejak nejde:)

1)Do extraktoru vstupují pokrutiny s obsahem 10% rostlin. Oleje. Olej je z pokrutin extrahován benzinem obsahujícím již na vstupu 0,5% oleje. Z extraktu vystupuje 500 kg pokrutin s obsahem 5% benzinu a 0,1% oleje. Extrakt. Benzin na výstupu obsahuje 40% oleje. Spočítejte, kolik pokrutin vstupuje v kg/hod. Do extraktu?

3) Je třeba připravit 1500 kg nitrační směsi o složení 56% kys. Sírové a 32% kys. Dusičné a 12% vody. K dispozici je 78% kys. Sírová a 78% kys. Dusičná. Jaká množství jednotlivých kyselin musí bý použita, lze směs připravit pouhým smícháním?

-tady sem si postupne udelal tamto jako v předchozich prikladech a kdyz udelam vzorec m3*w3=m1*w1+m2*w2 tak mi pořad vychazí 0 což je zrejme nesmysl. Tak že počítam špatně:D nebo to jde pouze tím smícháním?

ps: Jelena zase moc krat dik:)

jelena · 24. 10. 2008 00:04

↑ bons:

Zdravím :-)

předně děkuji za rozšíření mé slovní zásoby (netušila jsem, co je to "pokrutiny" a už to vím :-)

Samotný výpočet bude překvapivě jednoduchý, ale můžeme si nacvičit sestavování materialových bilancí:

http://forum.matweb.cz/upload/773-pokrutiny.JPG

a) co vstupuje:

x kg pokrutin, z toho 0,9x jsou "čisté" pokrutiny a 0,1x - rostlinný olej

y kg "olejnatého benzinu", z toho 0,005y - rostlinný olej a 0,995y - čistý benzin

b) co vystupuje

500 kg "benzinovo-olejnatých" pokrutin, z toho 0,05 * 500 = 25 kg benzinu a 0,001 * 500 = 0,5 kg zbytkového oleje, množství čistých pokrutin je (500-25-0,5 = 474,5 kg).

"benzino-olejová" směs, ve které je:

původní benzin po ztrátě 25 kg benzinu, co odešlo s pokrutinami, tedy (0,995y - 25) kg benzinu, benzin tvoří 60 % výstupní "benzino-olejové", jelikož dle zadání olej tvoří v směsi 40 % (proto oleje ve směsi je 40*(0,995y - 25)/60 kg)

Teď můžeš sestavovat bilance "vstup" = "výstup"...

Nám ovšem stačí začit od údaje o vstupu a výstupu "čistých" pokrutin:

0,9 x = 474,5
x = 527 kg - což je množství vstupujících pokrutin

Kontrolu můžeš provést přes bilanci oleje :-)

Nitrační směs

Dle zadání směs má obsahovat:

0,56 * 1500 = 840 kg sírové kyseliny (je to "čístá" kyselina bez vody)

0,32 * 1500 = 480 kg dušíčné kyseliny (také "čistá" kyselina)

0,12 * 1500 = 180 kg vody.

Budeme předpokladat, že pouze míchame kyseliny - to znamena, že společně s "čistou" kyselinou rostok už obsahuje vodu (22 % v původních roztocích kyseliny) a ověříme, zda je to možne:

Kyselina sirová (vnáší x g vody společně s roztokem), hmotnostní zlomek:
840/(840 + x) = 0,78, odsud množství vody x = 237 kg (je zřejmé, že pokud bychom míchali, tak už jen kyselina donese více vody, než je potřeba v roztoku)

480/(480+y) = 0,78, kyselina dusičná donese 135 kg vody (do potřebného množství vody chybí 45 kg vody).

Dopadne to asi tak, že kyselinu sírovou budeme muset vysušit do koncentraci 840/(840+45) = 95 %

Výpočet překontroluj pořádně s kalkulačkou, dost jsem zaokrozhlovala, aby bylo jednodušší pro čtení (a pokud mám nějaký překlep, tak se omlouvám :-)

-------------------------

Ještě k výpočtu parciálního tlaku (vše OK, pouze hodnota n=7,14 je počet molů. Ale výpočet v atm se mi nezdá, co se týče jednotek konstanty R, raděj bych vše převedla do SI)

bons · 24. 10. 2008 09:00

↑ jelena:
mam poznamku k tý nitrační směsi, v zadani je pravě "jake množství kyseliny je potřeba" to bylo poměrně snadné, m1=(1500*0,32)/0,78 tudíž m2=1500-m1
ale mám tu právě ulohu ze stejnými čísli ale bez jedny hodnoty jako v předešlí uloze, výsledky vim to je tech 615 a 885 ale jak k nim dojit prave:) v tom prave sem se zadrhl

Je třeba připravit 1500 kg nitrační směsi o složení 56% kys. Sírové a 32 % kys. Dusičné a 12% vody. Jakého množství kys. Musí být použito?
----------------------------------------------------------------------------

pak tady mam jen neco ke skontrolovaní:)
2) Z 82% roztoku kys. Sírové a vody je třeba připravit 200 kg o koncentraci 50%. Kolik kys. A vody musí být k přípravě roztoku použito?
m_3=200 kg......w_3=50%
m_1=x (kyseliny)......w_1=85%
m_2=200-x.......w_2=100% (prave sem nevim jestli dat 0% nebo 100% roztok vody)
m_3*w_3=m_1*w_1+m_2+w_2

počítam s 0%
200*0,5=0,85*x.........x=117,6 (taky zaokrouhluju)

ted ze 100%
200*0,5=0,85x+(200-x)*1....x=666,66666 (což je asi nesmysl)

--------------------------------------------------------------------------------
ještě poznamka k tomu tlaku, když tam mam 9atm tak ten vzorecek bude vypadak nějak takhle p=(9*nRT)/V ?

Cheop · 24. 10. 2008 10:32

↑ bons:
Musíš dát % vody = 0
Máš ve svém výpočtu chybu koncentrace kyseliny není 85 %, ale dle zadání 82 %.
(ale to je zřejmě jen překlep)
Pak to vyjde :
x = 122 (přibližně)

To znamená, že dáme 122 kg kyseliny v koncentraci 82 %
a 78 kg vody v koncentraci 0 % a dostaneme 200 kg roztoku o "síle" 50 %.

jelena · 24. 10. 2008 11:08 — Editoval jelena (24. 10. 2008 11:15)

↑ Cheop:

Srdečně zdravím, k nápovědě nemám jedinou připomínku :-)

↑ bons:

Pozdrav :-)

Napíš, prosím, konkrétní zadání (těžko vyluštím, bez kterého údaje to mám počítat) a, pokud máš, i výsledek.

Pokud je náhled na vzorová řešení, tak bych se docela rada podívala. OK?

Editace: do vzorce parciálního tlaku nepatri 9 atm. Pro kontrolu, zda je parciální tlak vypočten dobre slouží to, že parciální tlak musí být menší, než celkový tlak smesi.

bons · 24. 10. 2008 12:57 — Editoval bons (24. 10. 2008 13:10)

↑ jelena:
Zdravim:)
Jestli myslíš zadaní tak tohle je komplet zadani:

Je třeba připravit 1500 kg nitrační směsi o složení 56% kys. Sírové a 32 % kys. Dusičné a 12% vody. Jakého množství kys. Musí být použito?

Výsledky nemam...

zkoušel jsem to řešit asi takhle ale to je jen muj odhad..
víme ze zadaní že:
H2SO4 musí mít konečnou koncentraci 56% což je 840 kg
HNO3 musí mít 32% což je 480 kg
H2O 12% 180kg

m(H2SO4 a HNO3) to vlastne nezname, me napadlo že bych ke každy ty kyselině dal 6% vody takže vysledky by byly asi 930 h2so4 a 570 hno3. Tohle je jen moje uvaha:D

-----------------------
ještě takova menší poznamka v čem vychází parciální tlak?:D

jelena · 24. 10. 2008 16:41

↑ bons:

Je třeba připravit 1500 kg nitrační směsi o složení 56% kys. sírové a 32 % kys. dusičné a 12% vody. Jakého množství kys. musí být použito?

Smes má obsahovat:

0,56 * 1500 = 840 kg sírové kyseliny (je to "čístá" kyselina bez vody)

0,32 * 1500 = 480 kg dušíčné kyseliny (také "čistá" kyselina)

0,12 * 1500 = 180 kg vody.

V zadání není zadano, zda kyselina má být určité koncentraci. V tomto případě postupuji takto:

vodu (180 kg) mohu rozdelit třeba tak, že předpokládam kyseliny o stejné koncentraci (hmotnostní zlomek sírové = hmotnostní zlomek dusíčné)

w_1 = w_2

840/(840+x) = 480/(480+(180-x)) a z toho dopočítam x (množství vody v roztoku každé kyseliny a následně skutečnou koncentraci kyseliny)

Nebo vycházím z nabídky na skladě, ktery plním třeba z Prechezy a.s. a Proximu :-)

OK?

parciální tlak v atm (pokud se používá R = 0,082, ale nejak to nevychází), proto bych všechno převedla do SI, R = 8,31 a tlak bude v Pa.

OK?

bons · 24. 10. 2008 18:05

Ja se zatim nepodival jak se prevadi do SI jednotek ale to mi asi bude stacit takže R=8,31 T je v zadani a n si spocitam ty moly s enejak neprevadi ne?:) nebo objem?

jinak je to vsecko a mockrat dekuju:)

jelena · 26. 10. 2008 12:26

↑ bons:

Parciální tlak se vypočte dle vzorce:

$p_1=\frac{n_1RT}{V_{smesi}}$

n_1 - počet molů toho plynu, jehož parciální tlak počítame (pro výpočet počtu molů musíme dodržet stejné jednotky pro hmotnost plynu (u nás 200 g) a pro molární hmotnmost plynu (u nás 28 g/mol), ve výsledku dostaneme 7,14 mol

Ale na R musíme dát pozor. V zadání máš R= 0,082 a je to v jednotkách $\frac{dm^3\cdot{atm}}{K\cdot{mol}}$ - zřejmě se předpokládá, že to umíte nazpámě?, já jsem musela dohledat :-)

A zádrhel je pravě v tom, že v tomto zápisu R se vyskytuje dm^3, proto i zadaný objem musíme převest na dm^3.

$p_1=\frac{7.14\cdot{0.082}\cdot{293}}{1000}=0.172 \ atm$

Pokud počítame v SI: R=8,31 J/(K.mol), atmosfery je potřeba převádět do Pa, zbytek dle zadání.

Pro doplnění - obsah dusíku ve směsí je 0,172*100/9 = 1,9 %

jelena · 02. 01. 2013 21:51

Pro kolegyňku marie008 - z PM:

pokud mám zadanou konstantu R = 0,082 s jednotkou (l.atm/mol.deg), není mi jasné, zda mám nebo nemám převádět teplotu ze °c na Kelviny. Výsledný tlak by měl být v atm.?

O převodu jednotek je v příspěvku. Případně se ještě ozvi, zda to stačilo.

Téma přesunu do Chemie, ať mám na očích. Sekci biologie ještě nemáme ↑ kaja.marik: :-)

marie008 · 04. 01. 2013 18:51

↑ jelena:

Moc moc děkuji,
vypadá to, že jsem výpočet provedla správně:), ale...

na celé věci je mi totiž největší záhadou to mol.deg v jednotce - pokud by tam byl K.mol, je mi to úplně jasný a o převodu ze °C na K bych nepochybovala,
ale s tím "deg" se nějak nemůžu srovnat, zvlášť když máme v dalších výpočtech na tepelné bilance zadané molární teplo s jednotkou kJ/kmol.deg a výpočet se provádí s teplotou ve °C

Z toho jsem dobře zmatena a nikde jsem nenašla, co to "deg" znamená:(...

jelena · 04. 01. 2013 20:09

↑ marie008:

není za co, to je dobře, že se podařilo :-)

Úlohy jsou ze sbírky od pana Richtera - používá ve sbírce deg? V předchozích výpočtech sice deg v plynové konstantě bylo, ale jednotky byly $\frac{dm^3\cdot{atm}}{K\cdot{mol}}$ ↑ příspěvek 18: a hlavní převod byl Pa na atm a m^3 na dm^3.

Já bych pro sebe "deg" považovala za stupně. Deg se zavádělo nějak tak (a snad ještě bude ve smyslu "tepelného rozdílu").

Smysl to má, protože když definujeme např. měrnou tepelnou kapacitu, tak mluvíme o ohřátí 1 kg látky o 1 stupeň (co je ve skutečnosti "rozdíl teplot"). Jelikož rozdíl teplot jak v K, tak i ve stupních C, je stejný ( $\Delta T=T_2-T_1=(t_2+273)-(t_1+273)=t_2-t_1=\Delta t$ ), potom není nutné převádět Celsia na Kelvina, pokud počítáme v úloze rozdíl, nebo pokud fyzikální veličina se vztahuje k rozdílu. Sama víš, že zadání C nebo K nevyžaduje přepočet např. "měrné tepelné kapacity".

Naopak, pokud je zadána teplota a ve výpočtu je použitá teplota (ne rozdíl teplot), převod je nutný do vzorce 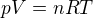$pV=nRT$ teplotu jedině v K.

Je to tak srozumitelné? Děkuji.

marie008 · 04. 01. 2013 22:47

↑ jelena:

Teď už je mi to úplně jasné, já trdlo jsem si vůbec neuvědomila, že v tom druhém případě jde o rozdíl teplot, kde je přepočet fakt zbytečný - uff, už taky dobře blbnu:)...

Úlohy jsou skutečně ze sbírky od p. děkana Richtera, ale tam jsem v jednotkách našla deg jen v jednom případě tepelné bilance.
Při výkladu pár vzorových příkladů na konzultaci (jsem dálkař po 20 letech od SŠ) mi to nějak v těch zadáních uniklo, takže jsem se hned nezeptala, a pak se v tom takhle ztrácím... občas je to samostudium docela náročné:)...

DĚKUJI MOC!!!

jelena · 04. 01. 2013 23:41

↑ marie008:

děkuji za zprávu, téma opět označím za vyřešené. Úloh ze sbírky je zde více a řekla bych, že převážně od dalkářů. Ať se vede v náročném samostudiu :-)

Matematické Fórum

#1 20. 10. 2008 10:50

slovní ulohy

#2 20. 10. 2008 13:02 — Editoval jelena (21. 10. 2008 23:15)

Re: slovní ulohy

#3 20. 10. 2008 17:38

Re: slovní ulohy

#4 20. 10. 2008 18:13 — Editoval kaja.marik (20. 10. 2008 18:14)

Re: slovní ulohy

#5 20. 10. 2008 18:28 — Editoval jelena (20. 10. 2008 18:30)

Re: slovní ulohy

#6 21. 10. 2008 16:42 — Editoval bons (21. 10. 2008 16:43)

Re: slovní ulohy

#7 21. 10. 2008 16:52

Re: slovní ulohy

#8 21. 10. 2008 23:35

Re: slovní ulohy

#9 22. 10. 2008 08:52

Re: slovní ulohy

#10 22. 10. 2008 09:36

Re: slovní ulohy

#11 24. 10. 2008 00:04

Re: slovní ulohy

#12 24. 10. 2008 09:00

Re: slovní ulohy

#13 24. 10. 2008 10:32

Re: slovní ulohy

#14 24. 10. 2008 11:08 — Editoval jelena (24. 10. 2008 11:15)

Re: slovní ulohy

#15 24. 10. 2008 12:57 — Editoval bons (24. 10. 2008 13:10)

Re: slovní ulohy

#16 24. 10. 2008 16:41

Re: slovní ulohy

#17 24. 10. 2008 18:05

Re: slovní ulohy

#18 26. 10. 2008 12:26

Re: slovní ulohy

#19 02. 01. 2013 21:51

Re: slovní ulohy

#20 04. 01. 2013 18:51

Re: slovní ulohy

#21 04. 01. 2013 20:09

Re: slovní ulohy

#22 04. 01. 2013 22:47

Re: slovní ulohy

#23 04. 01. 2013 23:41

Re: slovní ulohy

Zápatí