Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 01. 05. 2012 19:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vázané extrémy
Zdravím,
v rovnicích jsi ztratil  - nebyla viditelná, opravím . Máš soustavu 3 rovnice, 3 neznámé. Například druhou rovnici vynásobím (-1), sečtu s první. Podaří se dokončit? Děkuji.
- nebyla viditelná, opravím . Máš soustavu 3 rovnice, 3 neznámé. Například druhou rovnici vynásobím (-1), sečtu s první. Podaří se dokončit? Děkuji.
Offline
#4 01. 05. 2012 20:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vázané extrémy
↑ lajk:
já to vezmu jen slovně, neb se věnuji něčemu jinému.
Po úpravě ↑ jelena: vyjádřím  a dosadím do první a do druhé rovnice. Potom vynásobím celou rovnici jmenovatelem (který se objeví po vyjádření
a dosadím do první a do druhé rovnice. Potom vynásobím celou rovnici jmenovatelem (který se objeví po vyjádření  - je třeba ošetřit podmínky pro násobení).
- je třeba ošetřit podmínky pro násobení).
Nakonec v rovnicích (1), (2) budu mít  ,
, 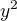 ,
, 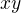 s nějakými koeficienty a vhodným vynásobením a sečtením rovnic odstraním
s nějakými koeficienty a vhodným vynásobením a sečtením rovnic odstraním 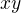 . V závěru bys měl mít poslední rovnici a ještě jednu, kterou vytvoříš po úpravách, jen s
. V závěru bys měl mít poslední rovnici a ještě jednu, kterou vytvoříš po úpravách, jen s  a
a 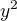 s nějakými koeficienty.
s nějakými koeficienty.
Případně se podívám tak po 22-23:00.
Offline
#6 01. 05. 2012 21:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vázané extrémy
Asi to nebyla ideální cesta, protože používáme pořád jen 2 rovnice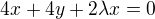
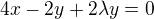
 (-y)
(-y) (x)
(x)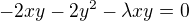
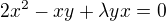
sečteme
-------------------------------------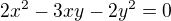 a vyřešíme jako kvadratickou rovnici vzhledem k x
a vyřešíme jako kvadratickou rovnici vzhledem k x , to už se dá používat do rovnice
, to už se dá používat do rovnice
Nemám nějakou chybu? Děkuji.
Offline
#8 01. 05. 2012 23:52
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: vázané extrémy
Zkus to překontrolovat tak:
dosazujeme x1=2y, dostaneme y_(1,2)=+/-1. Pro y=1, x=2. Pro y=-1, x=-2. Body [2, 1], [-2, -1] atd.
Mně se zdá těch bodů, co jsi vytvořil, nějak moc. je tak?
Offline