Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 05. 2012 15:28 — Editoval eldest (22. 05. 2012 15:28)
Planimetrie + stejnolehlost
Dobrý den,
chtěl bych se zeptat, zda někdo neví, jak vyřešit konstrukčně tento příklad:
Je dána kružnice k (S,r) a uvnitř ní bod M.Sestrojte všechny tětivy XY kružnice k, které procházejí bodem M tak, že bod M dělí tětivu XY v poměru 3:1.
Hlavně bych ho potřeboval vysvětlit, zkoušel jsem rektifikační úhel + to otočit v poměru 3:1, ale nevím jak dál.
Děkuju za případné odpovědi.
Pokud jsem Vám pomohl vyřešit příklad, dejte prosím palec :)
Offline
tak nedostal by si dva body v ktorých by sa ti pretli tieto dve kružnice?#4 22. 05. 2012 16:05
Re: Planimetrie + stejnolehlost
↑ Rumburak:
No a právě to nevím jak udělat.
↑ gogy27:
To nevím, je to maturitní příklad, potřebuju to vysvětlit a hlavně myslím, že bych měl použít stejnolehlost.
Pokud jsem Vám pomohl vyřešit příklad, dejte prosím palec :)
Offline
#7 22. 05. 2012 16:46
Re: Planimetrie + stejnolehlost
↑ Rumburak:
V tom som si nebol istý, počítal som to takto. Celá úsečka - 4časti, teda tá časť, kde je tá menšia časť by mala byť 
ale to je asi zla úvaha.
Offline
#9 23. 05. 2012 09:23 — Editoval Rumburak (23. 05. 2012 09:44)
Re: Planimetrie + stejnolehlost
↑ gogy27:
Koeficient stejnolehlosti f má kladné znaménko, když bod X'=f(X) , kde X<>M , leží na polopřímce MX (M je střed stejnolehlosti a zároveň
počáteční bod polopřímky MX) . Jestliže MX, MX' jsou opačné polopříkmy, pak koeficient stejnolehlosti je záporný. Plyne to z faktu, že
stejnolehlost o středu M a koeficientu k <> 0 je určena rovnicí 
.
Offline
#10 23. 05. 2012 09:43
Re: Planimetrie + stejnolehlost
↑ eldest:
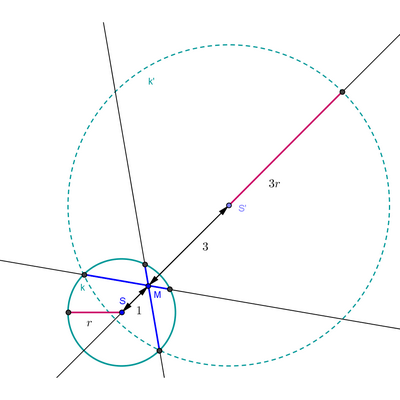
Na polopřímce opačné k polopř. MS (S je střed kružnice) sestrojíš bod S' tak, aby |MS'| = 3|MS| (pak bod M bude dělit úsečku SS' v poměru 1:3)
a okolo bodu S' opíšeš kružnici o poloměru 3r (r je poloměr první kružnice) . Pokud obě kružnice budou mít nějaký společný bod Y, najdeš jeho stejnolehlý
vzor X na první kriužnici (při téže stejnolehlosti). Úsečka XY bude tětivou první kružnice a bod M ji bude dělit v poměru 1:3.
Úloha může mít 0, 1 nebo 2 řešení - v závislosti na poloze bodu M.
Offline
