Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 06. 2012 12:09 — Editoval vanok (14. 06. 2012 12:10)
zabavne cvicenie: grupy
Pozdravujem.
Ako vyriesit toto? je konecna komutativna grupa.
je konecna komutativna grupa.
Urcite sucin vsetkych jej prvkov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 14. 06. 2012 13:13
Re: zabavne cvicenie: grupy
Offline
#3 14. 06. 2012 13:22
Re: zabavne cvicenie: grupy
↑ Rumburak:,
Pozdravujem,
oznacme ho napriklad 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 14. 06. 2012 23:54 — Editoval OiBobik (15. 06. 2012 12:05)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: zabavne cvicenie: grupy
↑ vanok:
Ahoj,viděl bych to takto:
Pěkný příklad. Trochu připomíná důkaz Wilsonovy věty.
Ještě mě k tomu napadá:
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#5 15. 06. 2012 12:22 — Editoval vanok (15. 06. 2012 13:18)
Re: zabavne cvicenie: grupy
Ahoj ↑ OiBobik:,
Pekne riesenie a sa podoba mojmu
Pre porovnanie si ho mozes tu precitat
edit: doplnenie posledneho vzorca
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 15. 06. 2012 12:37 — Editoval OiBobik (15. 06. 2012 12:41)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: zabavne cvicenie: grupy
↑ vanok:
Dotaz: Nepřepsal ses nějak v onom posledním řádku? Tuším, že vím, jak to myslíš, ale takto mi to nedává moc smysl,
Jinak moc hezký důkaz, zvlášť proto, že nepoužívá takové silné věty, jako ten můj,
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#7 15. 06. 2012 13:09 — Editoval vanok (15. 06. 2012 13:19)
Re: zabavne cvicenie: grupy
to je v jadre a tak mame uz
a tak mame uz 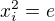 , a pre ten sucin mas pravdu.. to opravim.
, a pre ten sucin mas pravdu.. to opravim.
No ale je v podstate na tej istej myslienke ako tvoj ... az na to ze som trosku viac vyuzil komutativitu grupy.
Inac na tvoju otazku o grupach, kde 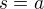 je asi uzitocne pozriet na klasifikaciu komutativnych grup.
je asi uzitocne pozriet na klasifikaciu komutativnych grup.
A este iny otvoreny problem: aky je obraz "takych" sucinov nekomutativnej grupy ( aspon pre male kardinality)?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 15. 06. 2012 13:28 — Editoval OiBobik (15. 06. 2012 14:01)
#9 15. 06. 2012 14:10
Re: zabavne cvicenie: grupy
↑ OiBobik:
No sme dokazali
Ak  ma dva rozne prvky,
ma dva rozne prvky, 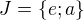 , kde
, kde 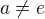 , mame
, mame 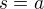
Ale si sa pytal v tvojom rieseni, ake su to presne groupy.
Si sa pytal, ci take grupy musia byt cyklicke:↑ OiBobik:
Mam priklad jednej necyklickej takej grupy.
Som isty, ze ho najdes aj ty.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 15. 06. 2012 14:17 — Editoval OiBobik (15. 06. 2012 14:21)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: zabavne cvicenie: grupy
↑ vanok:
Ano, máš pravdu.
Tady píšu charakterizaci těch grup ↑ OiBobik:.
Z toho, co tam píšu, neplyne, že by ty grupy musely být cyklické: Namátkou třeba 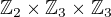 ... ta má právě jednu involuci
... ta má právě jednu involuci 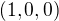 (neboli, v terminologii, používané tebou,
(neboli, v terminologii, používané tebou, 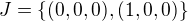 ). Takže pro ni to nutně platí.
). Takže pro ni to nutně platí.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#11 15. 06. 2012 15:38
Re: zabavne cvicenie: grupy
↑ OiBobik:
Moj priklad, je  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 15. 06. 2012 15:42 — Editoval vanok (15. 06. 2012 15:45)
Re: zabavne cvicenie: grupy
↑ OiBobik:
Moj priklad, je  .
.
A toto,
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
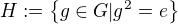 je množina všech involucí spolu s jednotkou. Pak jistě
je množina všech involucí spolu s jednotkou. Pak jistě  tvoří podrupu
tvoří podrupu  - jednotka náleží do
- jednotka náleží do 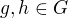 , pak
, pak  , jelikož
, jelikož 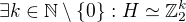
 pro
pro 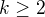 (stačí spočítat, že počet prvků, jež mají v i-té složce vektoru 1, je
(stačí spočítat, že počet prvků, jež mají v i-té složce vektoru 1, je  - což je sudé číslo, tedy
- což je sudé číslo, tedy  ). Tedy nutně
). Tedy nutně  , pokud
, pokud  .
.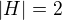 , pak je součin triviálně roven této jediné involuci grupy (tento případ může nastat - např. pro dvouprvkovou grupu).
, pak je součin triviálně roven této jediné involuci grupy (tento případ může nastat - např. pro dvouprvkovou grupu).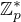 , a vůbec všechny cyklické grupy sudého řádu, jsou ostatně dobrý příklad oněch komutativních grup, pro něž tento součin (resp. součet) nebude jednotka (resp. nula). Celkem by mě zajímalo, jestli to jsou všechny příklady, nebo existují ještě jiné.
, a vůbec všechny cyklické grupy sudého řádu, jsou ostatně dobrý příklad oněch komutativních grup, pro něž tento součin (resp. součet) nebude jednotka (resp. nula). Celkem by mě zajímalo, jestli to jsou všechny příklady, nebo existují ještě jiné. 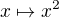 (to je morfismus groupy
(to je morfismus groupy  je sucin prvkov
je sucin prvkov 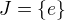 , je jasne, ze
, je jasne, ze 
 podgroupu jadra
podgroupu jadra 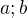 nie su rovnake a su obidvba rozne od
nie su rovnake a su obidvba rozne od 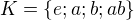
 taka, ze
taka, ze 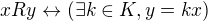 nam umoznuje partitionovat (rozrezat na triedy) jadro
nam umoznuje partitionovat (rozrezat na triedy) jadro 
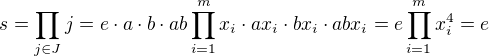
 ,
,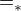 spočívá právě v tom přeskupení podle tříd ekvivalence?
spočívá právě v tom přeskupení podle tříd ekvivalence? pro
pro  liché.
liché. , kde
, kde 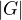 má jedinou involuci právě, když
má jedinou involuci právě, když  a
a 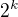 .
.