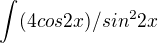Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 07. 2012 20:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: úprava integrálu
použit vzorec pro dvojnásobný úhel jak v čitateli (pro cos(2x)), tak i v jmenovateli pro sin(2x), potom opět dělení člen po členu.
V pořádku? Děkuji.
k zápisu - zlomek zapisujeme tak (v Editoru je to x/a)
Code:
\frac{4\cos (2x)}{\sin^2(2x)}Offline
#4 05. 07. 2012 20:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: úprava integrálu
↑ sparky29:
já už Tebe přenechám kolegům, výchovnou práci jsem provedla :-)
napíšeš  a rozložíš vnitřek.
a rozložíš vnitřek.
Offline
#5 09. 07. 2012 10:44 — Editoval Rumburak (09. 07. 2012 10:47)
Re: úprava integrálu
↑ sparky29:
Tady nejrychleji povede k cíli vnuknutí vyplývající z určité zkučenosti. Onu užitečnou zkušenost získáš, když si zderivuješ funkci  pro přípustná
pro přípustná  .
.
Offline
#6 09. 07. 2012 11:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: úprava integrálu
↑ Rumburak:
:-) ne-ne, kolega požadoval úpravou integrandu, tak jsem nabízela úpravy.
Ale už se se mnou nebaví, neb mu místo opravdu odborné pomocí uděluji jen rady do života. A já jsem pro něho měla ještě takových dobrých a užitečných rad :-)
Offline
#7 09. 07. 2012 11:23
#8 09. 07. 2012 11:32
Re: úprava integrálu
↑ jelena:
Geniální anekdota, tak dobrou jsem už dlouho neslyšel. :-)
Kolega tazetal snad tráví tyto prázdninové dny někde mimo dosah internetu a až se vrátí, dialog možná zase obnoví.
I když - na druhou stranu - komu je příjemné být vychováván ? :-)
Ahoj - přeji pěkné léto a dík za milý humor. :-)
Offline
#9 09. 07. 2012 14:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: úprava integrálu
↑ Rumburak:
děkuji :-) To je zlatý fond humoru (teď ale z hlavy neřeknu, zda byl u Poláčka nebo u F. Kafky nebo v knize). Až budu na druhé straně Opavy, tak upřesním ve správném tématu :-) Definitivní konec OT.
Offline