Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 07. 2012 16:40
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Analyticka geometria
Napíšte rovnicu kružnice ktorá sa dotýka priamok p : 3x - 4y + 1 = 0 a q: 3x - 4y + 5 =0. Ich stred leží na priamke j: 3x+2y = 0
Mam všetko urobene len polomer som počítal najprv inak trochu a nechcelo mi vysjť. ![kopírovat do textarea $S[-\frac{1}{3},\frac{1}{2}]$](/mathtex/58/586759f96043d9d54bcc96e4567d24fa.gif)
![kopírovat do textarea $L[x,\frac{3x+1}{4}]$](/mathtex/54/54cc259a001d7ea33c988f39942e3437.gif)

![kopírovat do textarea $K[x,\frac{3x+5}{4}]$](/mathtex/7e/7e80dcd03f49c29830b1252659117e18.gif)
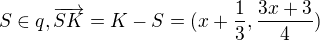
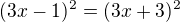
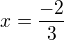
a nie a nie vyjsť.
Viem, že sa dá ľahko vypočítať cez vzdialenosť bodu od priamky.
Offline
- (téma jako vyřešené označil(a) miso16211)
#2 23. 07. 2012 19:17 — Editoval Cheop (23. 07. 2012 19:39) Příspěvek uživatele Cheop byl skryt uživatelem Cheop. Důvod: Špatná rada
#3 23. 07. 2012 20:26 — Editoval Cheop (23. 07. 2012 20:40)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Analyticka geometria
↑ miso16211:
Vzdálenost středu S od jedné z rovnoběžek bude hledaný poloměr
(Řešíš tedy úlohu vzdálenost bodu od přímky)
Aha takže jinak:
1) Urči rovnici přímky kolmé k jedné z rovnoběžek procházející středem S
2) Urči průsečík těchto 2 přímek
3) Hledaný poloměr bude vzdálenost středu S od průsečíku z bodu 2)
Nikdo není dokonalý
Offline
#4 23. 07. 2012 21:06
#5 23. 07. 2012 22:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analyticka geometria
↑ miso16211:
Zdravím, Mišo,
u Tvého řešení by bylo dobré slovně okomentovat, co jsi dělal a jaký smysl má každý výpočet. Tak jsem nedokázala posoudit, o co šlo. Nevím, zda kolegové?
Bod ![kopírovat do textarea $S[-\frac{1}{3},\frac{1}{2}]$](/mathtex/58/586759f96043d9d54bcc96e4567d24fa.gif) náleží přímce, na které má podle zadání být střed? Proč jsi zvolil zrovna takový bod, nebo je to výsledek výpočtu?
náleží přímce, na které má podle zadání být střed? Proč jsi zvolil zrovna takový bod, nebo je to výsledek výpočtu?
V případě rovnoběžných přímek (a třetí k ním nerovnoběžné) také můžeš najít průsečíky této přímky s rovnoběžkami a vypočíst střed takové úsečky (zároveň střed hledané kružnice), ale to jste už asi okomentovali s kolegou ↑ Cheop:.
Offline
#6 24. 07. 2012 09:49 — Editoval miso16211 (24. 07. 2012 13:00)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Analyticka geometria
![kopírovat do textarea $S[-\frac{1}{3},\frac{1}{2}]$](/mathtex/58/586759f96043d9d54bcc96e4567d24fa.gif) //stred kružnice som vypočítal ako priesečnik priamky j a priamky m - os pasa 3x - 4y + (6/2) =0 ô 3x - 4y + 3 =0
//stred kružnice som vypočítal ako priesečnik priamky j a priamky m - os pasa 3x - 4y + (6/2) =0 ô 3x - 4y + 3 =0![kopírovat do textarea $L[x,\frac{3x+1}{4}]$](/mathtex/54/54cc259a001d7ea33c988f39942e3437.gif) // leží ma priamke p, teda každy bod musi mať takéto suradnice, v takom "pomere"
// leží ma priamke p, teda každy bod musi mať takéto suradnice, v takom "pomere"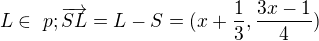 // vektor SL
// vektor SL ![kopírovat do textarea $K[x,\frac{3x+5}{4}]$](/mathtex/7e/7e80dcd03f49c29830b1252659117e18.gif) // bod patriaci priamke q, teda každy bod musi mať takéto suradnice, v takom "pomere"
// bod patriaci priamke q, teda každy bod musi mať takéto suradnice, v takom "pomere"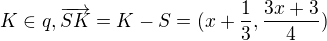 // vektor KS
// vektor KS  // velkosti vektorov sa rovnajú
// velkosti vektorov sa rovnajú =
= 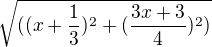 // vykratim odmocninu a
// vykratim odmocninu a  na oboch stranach sa vykráti.
na oboch stranach sa vykráti. 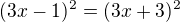
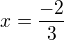 // x keď dosadim do vektora SK alebo SL a vypočítam jeho veľkosť (velkosť daného vektora) dostanem r - polomer kružnice
// x keď dosadim do vektora SK alebo SL a vypočítam jeho veľkosť (velkosť daného vektora) dostanem r - polomer kružnice
PS.: Nemôžem editovať to, čo som včera napísal :(, môže to byť kvôli zmene titulku?
Offline
#7 24. 07. 2012 10:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analyticka geometria
↑ miso16211:
Děkuji, Mišo,
ale
stred kružnice som vypočítal ako priesečnik priamky j a priamky q
asi nebude správný výchozí krok, protože jsi našel bod  (a označuješ ho za střed kružnice), který zároveň leží na přímce q. Podle zadání však kružnice se středem S se má přímky q dotykat. Pokud střed je na přímce q, tak se kružnice přímky q dotykat nebude.
(a označuješ ho za střed kružnice), který zároveň leží na přímce q. Podle zadání však kružnice se středem S se má přímky q dotykat. Pokud střed je na přímce q, tak se kružnice přímky q dotykat nebude.
Je to tak? Nebo jsem špatně pochopila? Děkuji.
Offline
#8 24. 07. 2012 10:22 — Editoval Rumburak (24. 07. 2012 10:24)
Re: Analyticka geometria
↑ miso16211:
Ahoj.
Kolegyně Jelena (již zdravím :-)) už objevila chybu. Proto já nyní už jen napovím snadný způsob řešení:
Střed kružnice leží zároveň na jisté přímce  , o níž se v zadání nehovoří.
, o níž se v zadání nehovoří.
Offline
#9 24. 07. 2012 10:25
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Analyticka geometria
↑ miso16211:
Pokud dosadím do Tvého výpočtu dostanu:
Výpočet
Nikdo není dokonalý
Offline
#10 24. 07. 2012 13:01
#11 24. 07. 2012 13:31 — Editoval Cheop (24. 07. 2012 13:32)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Analyticka geometria
↑ Rumburak:
Zdravím:-)
Střed bude ležet na přímce uprostřed těch rovnoběžek
A bude to průsečík této přímky s přímkou 3x + 2y=0
(Ale to Ty jistě víš)
Nikdo není dokonalý
Offline
#12 24. 07. 2012 14:42
Re: Analyticka geometria
↑ Cheop:
Ahoj, přesně tak. Užitečné je uvědomit si, že když p : 3x - 4y + 1 = 0 , q: 3x - 4y + 5 =0, potom přímka w , která je s nimi rovnoběžná
a leží "uprostřed mez nimi", má rovnici p : 3x - 4y + 3 = 0 (protože (1+5)/2 = 3 ).
Offline
#13 24. 07. 2012 18:14
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Analyticka geometria
↑ Rumburak: šak hej, ale dal a dál moje riešenie nevychádza, a postup mam ako vy to tu píšete
Offline
#14 24. 07. 2012 19:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Analyticka geometria
↑ miso16211:
překontroluj, prosím, rovnici 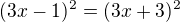 (na nový papír). Ať se podaří.
(na nový papír). Ať se podaří.
Offline
#15 25. 07. 2012 10:04 — Editoval Rumburak (25. 07. 2012 10:17)
Re: Analyticka geometria
↑ miso16211:
Máš pravdu. Vycházel jsem pouze z Tvého prvního příspěvku ↑ miso16211:, odkud mi jednotlivé kroky Tvého postupu nebyly srozumitelné.
Jak Ti vyšel kořen rovnice 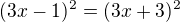 ? Mně
? Mně  . Ale k čemu Ti toto řešení bude ? Odpovídající body
. Ale k čemu Ti toto řešení bude ? Odpovídající body  na
na
přímkách  jsou takové, kreré mají stejnou x-ovou souřadnici jako bod
jsou takové, kreré mají stejnou x-ovou souřadnici jako bod  , což by Ti pro určení poloměru pomohlo pouze tehdy,
, což by Ti pro určení poloměru pomohlo pouze tehdy,
když přímka 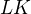 by zároveň byla kolmá k přímkám
by zároveň byla kolmá k přímkám  , to ale není náš případ .
, to ale není náš případ .
Ty potřebuješ nalézt takový bod  , aby vektor
, aby vektor 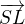 byl kolmý k přímce
byl kolmý k přímce  . Poloměrem kružnice pak bude
. Poloměrem kružnice pak bude 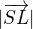 .
.
Ještě jedna POZNÁMKA k Tvému dosavadnímu postupu: Podmínku, že body  budou mít tutéž x-ovou souřadnici, jsi stanovil Ty sám - tím,
budou mít tutéž x-ovou souřadnici, jsi stanovil Ty sám - tím,
že jsi ji u obou těchto bodů označil toutéž proměnnou (x). Mohl jsi pro každý bod použít jinou proměnnou, ale tím bys dostal rovnici o dvou neznámých
a rovněž i zde bys musel použít podmínku na kolmost.
Offline
#16 25. 07. 2012 10:07 — Editoval miso16211 (25. 07. 2012 10:10)
#17 25. 07. 2012 10:12 — Editoval miso16211 (25. 07. 2012 10:21)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Analyticka geometria
↑ Rumburak: vypočítam cez x polomer kružnice.
x dosadím do jedného z vektorov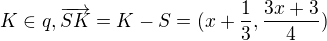
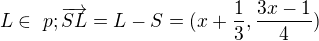
a vypočítam veľkosť vektora a mám polomer. Stred už dávno mám.
polomer má vyjsť r = 1,5 a mne vychádza 0,5
smerový vektor priamky p je s=(4,3)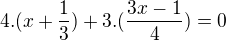 // smerový . kolmý = 0
// smerový . kolmý = 0
a toto mi nevychádza. či ako si to myslel.
Offline
#18 25. 07. 2012 10:29
Re: Analyticka geometria
↑ miso16211:
Až budeš mít nekterý z bodů K, L , pak už snadno spočteš poloměr kružnice (jako velikost vektoru K-S resp L-S), který nám dopod ještě chybí -
to je správná úvaha.
PS. Ale jak nalézt některý z bodů K, L se snad už mezitím vyjasnilo mým příspěvkem ↑ Rumburak: , do něhož jsem ještě něco doplnil.
Offline
#19 25. 07. 2012 10:40
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Analyticka geometria
↑ Rumburak: šak mam vektor a mi nevychádza. a načo mi bod K alebo L, staci mi vektor LS a jeho velkost.
Offline
#20 25. 07. 2012 11:01
Re: Analyticka geometria
↑ miso16211:
Ano, takto jsem to myslel . Vyšlo mi 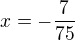 , což, pravda, není uklidňující mezivýsledek. Dále mi vychází
, což, pravda, není uklidňující mezivýsledek. Dále mi vychází  , jeho velikost
, jeho velikost 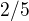 .
.
Kontrola: Ze vzorce pro vzdálenost dvou rovnoběžek vychází pro p, q hodnota 4/5 , takže předchozí výsledek je správně.
Offline
#21 25. 07. 2012 11:12 — Editoval Rumburak (25. 07. 2012 11:13)
Re: Analyticka geometria
↑ miso16211:
Body K, L určitě nepotřebujeme oba, ale pmocí bodu L můžeme vyjádřit vektpr L-S a nebo pomocí bodu K vyjádřit vektor K-S (rovněž kolmý
k daným rovnoběžkám) . Který z obou vektorů použijeme pro výpočet poloměru kružnice, je úplně jedno, můžeme si vybrat.
Offline
#22 25. 07. 2012 12:13
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Analyticka geometria
↑ miso16211:
Podle Tvého výpočtu jak vidíš ty rovnice nemohou platit - viz obrázek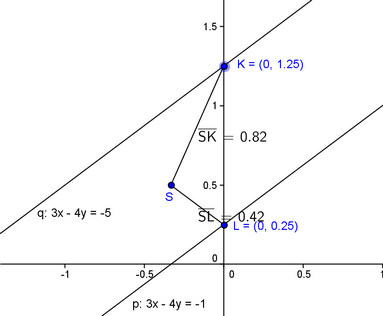
Nikdo není dokonalý
Offline
#23 25. 07. 2012 12:34
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Analyticka geometria
↑ Rumburak: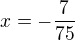
a mne to nevychádza, 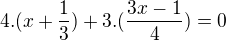
ked dosadim tvoj vysledok vychádza mi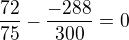
Offline
#24 25. 07. 2012 15:23
#25 25. 07. 2012 15:42
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Analyticka geometria
Ja tu ulohu viem, len som nevedel preco mi to nechce vysjt cez zlozitejsi postup. Teraz vidím že žložity postup je ešte zložitejším. Viem tu úlohu. Téma označujem ako vyriešenú.
Offline

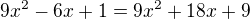 / + 6x, -9
/ + 6x, -9  / + 6x, -9
/ + 6x, -9
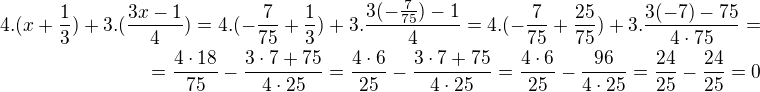 .
.