Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 09. 2012 16:58 — Editoval Anonymystik (04. 09. 2012 17:02)
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Japonské Sangaku
Zdravím. Japonská kultura byla pro nás, Evropany, vždy něčím zvláštní. Jeden z jejich dávných zvyků byl vyrývat na stěny chrámů geometrické obrazce, které vždy představovaly nějakou úlohu jako výzvu pro všechny bystré poutníky. Mezi tyto úlohy (tzv. Sangaku) patřila mimojiné i tato překrásná úloha:
Mějme tětivový čtyřúhelník ABCD. Dokažte, že platí následující tvrzení: rozřežeme-li čtyřúhelník úhlopříčkou AC a do dvou vzniklých trojúhelníků vepíšeme kružnice, tak součet jejích poloměrů bude stejný jako součet poloměrů kružnic vepsaným trojúhelníkům, které vzniknou při rozříznutí čtyřúhelníku úhlopříčkou BD.
Poznamenal bych, že ve skutečnosti je tvrzení obecnější a platí obecně pro triangluci libovolného tětivového n-úhelníků, ale i důkaz pro čtyřúhelník není zdaleka triviální (aspoň jsem žádný triviální nenašel).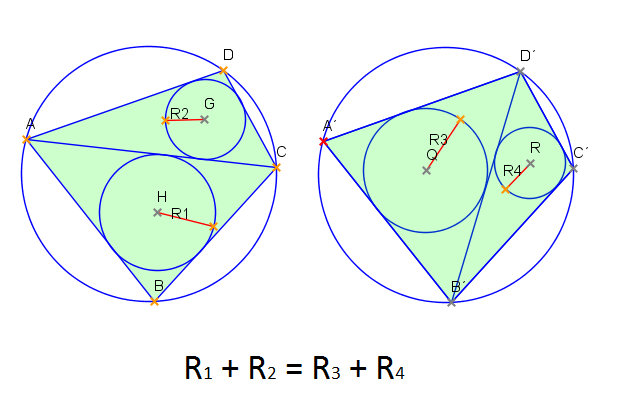
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#2 11. 09. 2012 13:20
Re: Japonské Sangaku
Ahoj ↑ Anonymystik:,
To je pekna iniciativa sa zaujimat o geometriu "sangaku", iste si si vsimol, ze v peknych teoremach som uz dal niekolko odkazov na tuto temu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 11. 09. 2012 18:25 — Editoval Anonymystik (11. 09. 2012 18:29)
- Anonymystik

- Příspěvky: 585
- Reputace: 45
Re: Japonské Sangaku
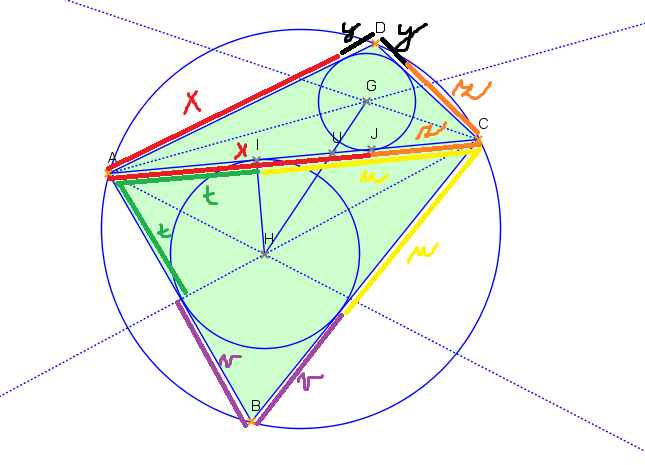
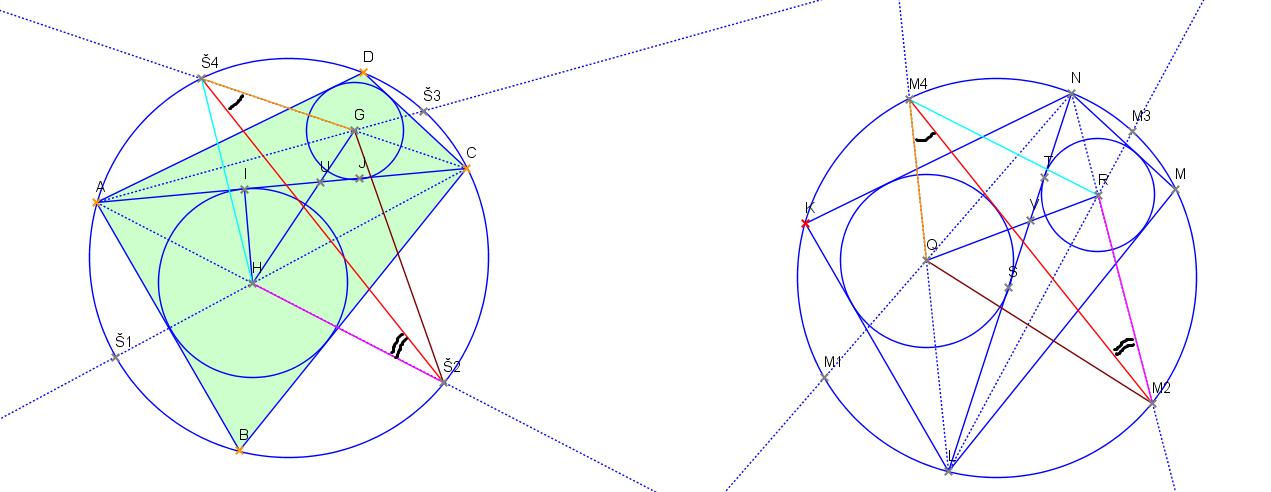
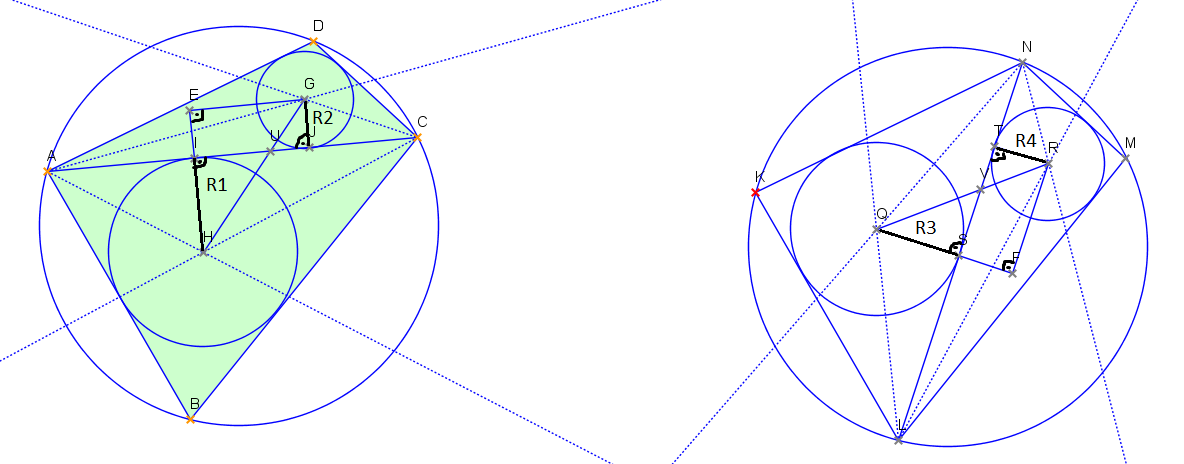
↑ vanok:↑ vanok: Ahoj. Tvůj důkaz bych uvítal rozepsaný. Zkoušel jsem na to tvůj vztah aplikovat, ale nic hezkého mi nevyšlo, tam mi asi něco ušlo. Jinak do hidu dám své řešení, vzhledem k tomu, že úloha tady leží už týden. Značení viz obrázek: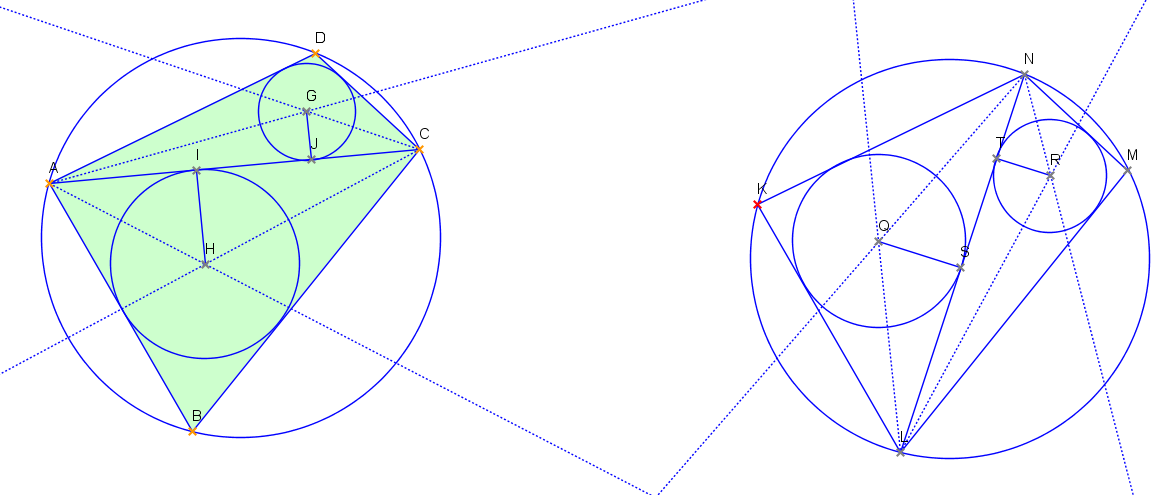
Část 1:
Část 2:
Část 3:
"Do you love your math more than me?" "Of course not, dear - I love you much more." "Then prove it!" "OK... Let R be the set of all lovable objects..."
Offline
#4 12. 09. 2012 13:53
Re: Japonské Sangaku
↑ Anonymystik:,
Ahoj, na moj dokaz ti pozem poslat, este male indikacie... vsak nie je vadcia radost ako ho sam najst.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 03. 11. 2012 13:26 — Editoval vanok (03. 11. 2012 13:26)
Re: Japonské Sangaku
Ahoj geometrici.
Posuvam tento pekny problem na vrch. .. Vsak ide o peknu geometriu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 (R=polomer opisanej kruznice , r= polomer vpisanej kruznice) ako aj Ptolemee-ovu teoremu ( pre konvexny vpisany srvoruholnik).
(R=polomer opisanej kruznice , r= polomer vpisanej kruznice) ako aj Ptolemee-ovu teoremu ( pre konvexny vpisany srvoruholnik).