Matematické Fórum

Brambor004 · 02. 10. 2012 23:41

Dobrý večer, nevím si rady s jedním příkladem, který jsem měl zadaný v písemce. Učitel mi odmítá podat vysvětlení, já už jsem zoufalý. Prosím, ukážete mi řešení? Netopýr vysílá ultrazvukový signál rychlostí 340m/s. Jeho rychlost je "P" m/s. Jak daleko je netopýr od překážky, když zvukový signál zaznamená "(P + J)/10" sekund po jeho vysílání?

Honzc · 03. 10. 2012 10:25 — Editoval Honzc (03. 10. 2012 10:58)

↑ Brambor004:
Předpokládám, že $J$ je rychlost signálu netopýra tj.340m/s

Autor skryl část textu. Zobrazit/skrýt!

Po editaci.
Nemá být náhodou ten čas zaznamenání signálu převrácená hodnota toho tvého výrazu
tedy $t=\frac{10}{J+P}$ (to by totiž dávalo smysl s ohledem na voreček $t=\frac{s}{v}$ )
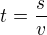Ono je totiž dost dobře nepředstavitelné, že kdyby netopýr letěl např. rychlostí 10 m/s, že by byl od překážky vzdálen skoro 6 km a na signál by čekal 35 s.
Pak by výsledek byl
$d=5\frac{J-P}{J+P}$ , což asi více odpovídá realitě.

zdenek1 · 03. 10. 2012 11:26

↑ Brambor004:

Na obrázku $v$ je rychlost ultrazvukového signálu.
Ten se k překážce (vzdálené $s$ ) šíří rychlostí $P+v$ a dorazí k ní za dobu $t=\frac{s}{P+v}$ .
Pak se začne vracet, ale protože se odrazil od nehybné překážky, vrací se už jen rychlostí $v$ .
Protože celková doba letu signálu byla $\frac{P+J}{10}$ , návrat trval $t^\prime=\frac{P+J}{10}-t=\frac{P+J}{10}-\frac{s}{P+v}$
a signál urazil dráhu $x=vt^\prime=\left(\frac{P+J}{10}-\frac{s}{P+v}\right)v$

Netopýr urazí dráhu $P\frac{P+J}{10}$ .

Musí proto platit
$s-P\frac{P+J}{10}=\left(\frac{P+J}{10}-\frac{s}{P+v}\right)v$
z této rovnice si vypočítáš
$s=\frac{(P+J)(P+v)^2}{10(P+2v)}$
A
$x=\frac{(P+J)(P+v)^2}{10(P+2v)}-P\frac{P+J}{10}=\frac{P+J}{10}\cdot \frac{v^2}{P+2v}$

Brambor004 · 05. 10. 2012 12:52

Ted mi to je alespon trochu jasne. Zkusim se na to jeste podivat a zjistit princip vztahu. Nechci to totiz proste opsat a rikat, ze to chapu. Moc dekuji.

Matematické Fórum

#1 02. 10. 2012 23:41

Mechanické vlnění

#2 03. 10. 2012 10:25 — Editoval Honzc (03. 10. 2012 10:58)

Re: Mechanické vlnění

#3 03. 10. 2012 11:26

Re: Mechanické vlnění

#4 05. 10. 2012 12:52

Re: Mechanické vlnění

Zápatí