Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 22. 11. 2008 11:30
Re: faktorial
Záleží na tom, co myslíš výpočtem faktoriálů. Mohl bys to prosím upřesnit?
Vzhledem ke vzorci, který uvádíš, předpokládám, že se jedná o to, nějak jednoduše vyčíslit daný výraz s kombinačními čísly. Vycházíme z vzorce pro kombinační číslo pro celá nezáporná n, k
Dosadíme-li tedy, dostaneme
Offline
#6 22. 11. 2008 12:33
Re: faktorial
Jo, spousta toho se tam pokrátí, ale stále mi tam vyskakují neuvěřitelné cifry, prostě nic, co by se dalo spočítat na papíře. Přiznávám, nevím, co dál.
Offline
#8 22. 11. 2008 14:07
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: faktorial
↑ Olin:
On výsledek není 0,004, ale  . Takže bych se počítáním na papír nezabýval.
. Takže bych se počítáním na papír nezabýval.
Offline
#9 22. 11. 2008 15:02
Re: faktorial
↑ BrozekP:
už jsem na to přišel, všem moc díky. Je to dost náročný ale dá se to spočítat na papíre ale bez kalkulačky ani ranu.
Offline
#10 22. 11. 2008 15:26
Re: faktorial
↑ Chrpa: ↑ BrozekP:
Asi tak, proč pak nepustit nějaký CAS a normálně do něj nenarvat původní zadání s kombinačními čísly? Je zbytečné cokoliv upravovat, když i to za nás mohou provést stroje.
Offline
#12 23. 11. 2008 14:56
Re: faktorial
↑ Chrpa:
Považuji.
Pokusím se můj postoj trochu objasnit. Podle zadání jde o to, vypočítat hodnotu výrazu s kombinačními čísly. Samozřejmě první co mě napadlo, bylo narvat to do kalkulačky nebo komplu. Jenže předpokládám, že to napadlo i zadávajícího, proto jsem chápal zadání tak, že se má výraz vyčíslit nějak elegantně, pomocí postupných úprav, kterými se dostaneme na nějakou snadno spočítatelnou hodnotu.
Analogicky - když se někdo zeptá třeba na toto: Kolik je  , tak taky asi neodpovím "hoď to do kalkulačky a uvidíš", ale ukážu, jak se to dá jednoduše vyčíslit pokrácením.
, tak taky asi neodpovím "hoď to do kalkulačky a uvidíš", ale ukážu, jak se to dá jednoduše vyčíslit pokrácením.
Offline

 .
.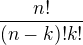 .
. , tak je to
, tak je to 