Matematické Fórum

martin333 · 31. 01. 2013 14:48

Prosím o pomoc pri dôkaze, že rad $\Sigma \frac{1}{2n+1}$ je divergentný. Hľadal som nejaký známy divergentný rad, aby som mohol použiť porovnávacie kritérium, ale nič som nenašiel...:(...

Wellcosh · 31. 01. 2013 15:01

$\sum {1 \over n}$ diverguje

martin333 · 31. 01. 2013 15:03

↑ Wellcosh:, ďakujem, to mi tiež napadlo... Harmonický rad... Tento je zjavne jeho časťou... Platí ale, že keď nejaký rad diverguje, že potom už diverguje aj jeho "podrad"?

Wellcosh · 31. 01. 2013 15:10

No, pro řady s nezápornými členy ano. Když má řada konečný součet a sečteš jenom nějakou podposloupnost, tak to pochopitelně nemůže být větší (mohlo by se stát, že řada nebude mít limitu (bude oscilovat), to ale u monotonní řady nastat nemůže).

Jinak tady se můžeš opřít o limitní srovnávací kriterium. Pokud jsou si posloupnosti 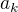$a_k$ a $b_k$ řádově rovny (v nekonečnu), tj.
$\exists c \in \mathbb{R} \setminus \{0\}: \lim_{k \rightarrow \infty} {a_k \over b_k} = c$ ,
pak $\sum a_k$ konverguje právě tehdy, když konverguje $\sum b_k$ .

martin333 · 31. 01. 2013 15:16

Ďakujem ↑ Wellcosh:, skúsim sa s tým nejako "zrovnať"...

Stýv · 31. 01. 2013 15:35

martin333 napsal(a):
Platí ale, že keď nejaký rad diverguje, že potom už diverguje aj jeho "podrad"?

takový nesmysl samozřejmě neplatí

Wellcosh napsal(a):
Když má řada konečný součet a sečteš jenom nějakou podposloupnost, tak to pochopitelně nemůže být větší ...

toto platí jenom pro nezáporné řady (možná jsi to tak myslel, ale radši se ujišťuju)

jarrro · 31. 01. 2013 19:56

čo je to podrad?
ak je to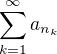
$\sum_{k=1}^{\infty}{a_{n_k}}$
kde n je rastúca postupnosť prirodzených čísel tak sa dá vymyslieť aj kladný rad divergentný rad s konvergentným podradom napríklad
$\sum_{k=1}^{\infty}{\frac{1}{k}}$
je divergertný ale jeho podrad
$\sum_{k=1}^{\infty}{\frac{1}{2^k}}=1$
je konvergentný

Wellcosh · 31. 01. 2013 20:05

↑ jarrro: Ale naopak to platit nemůže. Nemůže se "výběrem z řady" stát z konvergentní divergentní (pro řady s nezápornými členy).

jarrro · 31. 01. 2013 20:28

↑ Wellcosh:to nie ak je nezáporný rad konvergentný tak aj podrad je konvergentný to je jasné , ale martin333 sa pýtal či je podrad divergentného radu divergentný

martin333 napsal(a):
↑ Wellcosh:, ďakujem, to mi tiež napadlo... Harmonický rad... Tento je zjavne jeho časťou... Platí ale, že keď nejaký rad diverguje, že potom už diverguje aj jeho "podrad"?

ukázal som, že nemusí byť

Matematické Fórum

#1 31. 01. 2013 14:48

divergentný rad

#2 31. 01. 2013 15:01

Re: divergentný rad

#3 31. 01. 2013 15:03

Re: divergentný rad

#4 31. 01. 2013 15:10

Re: divergentný rad

#5 31. 01. 2013 15:16

Re: divergentný rad

#6 31. 01. 2013 15:35

Re: divergentný rad

martin333 napsal(a):

Wellcosh napsal(a):

#7 31. 01. 2013 19:56

Re: divergentný rad

#8 31. 01. 2013 20:05

Re: divergentný rad

#9 31. 01. 2013 20:28

Re: divergentný rad

martin333 napsal(a):

Zápatí