Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Wolfram alpha ortonormální báze (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 02. 2013 13:42
Wolfram alpha ortonormální báze
Ahoj, umí wolfram vypočítat ortonormální bázi generovanou 3 vektory? Pokud ano tak jak?
Věřím že umí, je to chytrej stroj :-)
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
- (téma jako vyřešené označil(a) PanTau)
#2 01. 02. 2013 14:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
Zdravím,
zadala jsem úlohu z této sbírky takovým způsobem (budeš muset okopírovat pro vložení "hranaté závorky v adrese"):
Code:
http://www.wolframalpha.com/input/?i=Orthogonalize[{{2%2C+4%2C+2%2C1}%2C+{-1%2C+-2%2C+-2%2C+-1}%2C+{1%2C+2%2C+4%2C+2}%2C+{1%2C+2%2C+3%2C+4}}](nech si ukázat Exact form). Vyhovuje tak? Děkuji.
Offline
#3 01. 02. 2013 16:59
Re: Wolfram alpha ortonormální báze
↑ jelena:
To je přesně ono, snad mi budou vycházet příklady stejně tak jako wolframu a bude to špičkové! Díky :-)
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#5 01. 02. 2013 17:51 — Editoval PanTau (01. 02. 2013 17:51)
Re: Wolfram alpha ortonormální báze
↑ jelena:
Když už jsme v tom, tak jsem to vyzkoušel,
Příklad :
Zadal jsem to na wolfram a vylezla mi nějaká kravina, ani nemám možnost nechat si ukázat Exact form.
Zadal jsem to správně? Platí takové zadání i pro vektory?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#6 01. 02. 2013 18:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
To bych řekla, že Exact form zrovna ukazuje. Jinak je kontrola (ruční), podle které poznáš, zda máš ortonormální bázi - zkus se ještě podívat do definice "ortonormální báze".
Offline
#8 01. 02. 2013 22:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
jak jsi přišel na to, že neumí? Pokud používáš Gram-Schmidt proces, tak první vektor překontroluješ jak? Co pro to potřebuješ aby WA pro kontrolu ještě dle Tvého pokynu spočítal?
A jak překontroluješ (za pomocí WA samozřejmě) další výsledky)?
Záleží na Tobě, zda ten výsledek vezmeš jako hotový, nebo nejsi si jistý a ještě překontroluješ - dle definice.
Offline
#9 02. 02. 2013 09:32
Re: Wolfram alpha ortonormální báze
↑ jelena:
Vypočítal jsem to pomocí Gram-Schmidtova procesu.
Vypočítal jsem
Kdy yn přestavují vektory







Za výsledek jsem označil v3, protože tak jsme to počítali ve škole,
Difinicí myslíš TOHLE? - pokud ano, z toho nevidím jak si udělat ,,zkoušku,,
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#10 02. 02. 2013 11:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
děkuji.
překontrolovala jsem 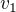 ,
, 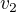 , skalární součin je 0, tedy podmínku "ortogonální" jsi splnil (další vektor vůči prvnímu a druhému překontroluj, prosím, sám).
, skalární součin je 0, tedy podmínku "ortogonální" jsi splnil (další vektor vůči prvnímu a druhému překontroluj, prosím, sám).
jelikož v zadání je najít ortonormální bázi, třeba použit normy vektorů (a potom budeš mít výsledek WA).
Ano, definici myslím, že překontrolujeme skalární součiny, zda nulové a normy vzniklých vektorů, zda jsou 1. V pořádku tak?
Pro zajímavost - tuto úlohu jsem již kontrolovala, ale špatně, ovšem kolega Kondr situaci napravil, děkuji :-)
Offline
#11 02. 02. 2013 11:56
Re: Wolfram alpha ortonormální báze
↑ jelena:
Pořád děkuješ, i když nevím za co, to já bych měl stále děkovat.
Skalární součin 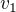 a
a 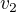 je opravdu
je opravdu 
Ale skalární součin 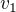 a
a 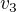 již 0 není - to znamená chybně vypočítané? Pochopil jsem to tak?
již 0 není - to znamená chybně vypočítané? Pochopil jsem to tak?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#12 02. 02. 2013 12:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
to se tak děkuje navzájem - v duchu návrhu (kolegovi Kondrovi děkuji, že ještě kontroloval, Tobě - že jsi si dal čas a přehledně napsal).
Mám dojem, že zde je chyba:
Ještě - píšeš, že za výsledek jsi označil 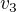 , to ne - výsledkem bude celá "ortonormální báze".
, to ne - výsledkem bude celá "ortonormální báze".
Offline
#13 02. 02. 2013 12:39
Re: Wolfram alpha ortonormální báze
Ano, přepočítal jsem  a vyšlo 0
a vyšlo 0
Po přepočtení vyjde 
Ještě - píšeš, že za výsledek jsi označil , to ne - výsledkem bude celá "ortonormální báze".
Co tedy označím za výsledek?
Na odkaz kolegi Kondra jsem koukal, nicméně jsem to nepochopil ani s ostatních vláken co tam navazují.
v duchu návrhu
Tím máš namysli že řešíme příklad ve špatné kategorii?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#14 02. 02. 2013 12:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
ještě jednou přepočti své skalární součiny pro  - např. pomoci WA. napíš, prosím, co jsi dosazoval, protože mně to vychází jinak.
- např. pomoci WA. napíš, prosím, co jsi dosazoval, protože mně to vychází jinak.
Tím máš namysli že řešíme příklad ve špatné kategorii?
:-) to už bych Tebe dávno přesunula. My jsme začali od užití WA a pokusíme se ukázat použití WA pro různé etapy kontroly Tvé úlohy. Potom si také řekneme, co je výsledek celé úlohy.
Offline
#15 02. 02. 2013 13:02
Re: Wolfram alpha ortonormální báze
↑ jelena:
Jsem rád že se mnou tak hezky diskutuješ.





Ověřeno i přes WA
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#16 02. 02. 2013 13:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
děkuji, už mi všechno sedí (neumím 2+8-7), vektory jsou k sobě kolmé po dvojicích - souhlasí? Snad jsi s kontrolou nezabil moc času.
Máme už ortogonální bázi 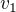 ,
, 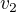 ,
, 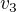 , zbývá najít normy jednotlivých vektorů a převést na ortonormální.
, zbývá najít normy jednotlivých vektorů a převést na ortonormální.
Offline
#17 02. 02. 2013 13:32
Re: Wolfram alpha ortonormální báze
vektory jsou k sobě kolmé po dvojicích
Kolmé = skalární součin obou = 0
Je tomu tak..?
Takže, ortogonální bázi tvoří 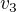
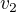
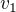
zbývá najít normy jednotlivých vektorů a převést na ortonormáln
Ale jak na to?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#18 02. 02. 2013 14:02
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
ano, kolmost jsem ověřovala pomocí skalárního součinu. Normalizace - dle 2. kroku v odkazu ("každý vektor vydělíme jeho normou" (c)).
Offline
#19 02. 02. 2013 14:32
Re: Wolfram alpha ortonormální báze
↑ jelena:
Takže..





Pokud jsem zase nikde nic nepomotal, tak by to mělo být takhle..
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#20 02. 02. 2013 14:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
co se tak zběžně dívám na výsledek WA ↑ příspěvek 5:, tak po podělení normou jste ve shodě - je to tak?
Offline
#21 02. 02. 2013 14:43 — Editoval PanTau (02. 02. 2013 15:00)
Re: Wolfram alpha ortonormální báze
↑ jelena:
Ale jaktože Výsledek na wolframu obsahuje v kolence result 4, 4prvkové závory..?
Vždyť my máme 3 prvky..?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#22 02. 02. 2013 15:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
my máme v zadání 3 vektory  (každý vektor má 4 složky - v závorce), Ty jsi po ortogonalizaci dostal vektory
(každý vektor má 4 složky - v závorce), Ty jsi po ortogonalizaci dostal vektory 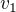 ,
, 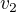 ,
, 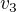 (každý má opět 4 složky). Měli jsme možná nové vektory označit úplně jinak, protože nějaké v již v označení máme, ale nevadí.
(každý má opět 4 složky). Měli jsme možná nové vektory označit úplně jinak, protože nějaké v již v označení máme, ale nevadí.
teď vektory 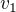 ,
, 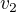 ,
, 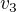 každý podělíš jeho normou a dostaneš ortonormální bázi, označ si ji třeba
každý podělíš jeho normou a dostaneš ortonormální bázi, označ si ji třeba 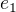 ,
,  ,
,  . A to je totéž, co má WA ve 3 velkých závorkách (,,,), v každé má 4 prvky.
. A to je totéž, co má WA ve 3 velkých závorkách (,,,), v každé má 4 prvky.
Co jsme prakticky dělali, je dobře vidět na obrázcích z ruské Wikipedie, ale když Ty jsi měl potíž se slovanskými jazyky :-)
V pořádku už?
Offline
#23 02. 02. 2013 15:15
Re: Wolfram alpha ortonormální báze
↑ jelena:
Ahá, tak již to chápu a to 100%.
Děkuji za vysvětlení a čas věnovaný mě......
Škoda že já tobě takhle nikdy nepomůžu a tak ti to neoplatím.
Díky :-)
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#24 02. 02. 2013 18:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Wolfram alpha ortonormální báze
↑ PanTau:
tak to je dobře, děkuji za zprávu.
Škoda že já tobě takhle nikdy nepomůžu a tak ti to neoplatím.
to nijak nevadí - všimni si, že v tématu působím minimálně a v podstatě všechno uděláš sám, zpětnou odezvu mám a téma je označeno za vyřešené. Tedy naprostá spokojenost z mé strany (až na detail - "věnovaný mně :-)
Offline
Stránky: 1
- Hlavní strana
- » Počítačové algebraické systémy (CAS)
- » Wolfram alpha ortonormální báze (TOTO TÉMA JE VYŘEŠENÉ)


