Matematické Fórum

Diamanticek1 · 28. 03. 2013 11:49

Zdravím vás :) Koukám, že už tu jedno podobné téma je, ale stejné příklady jsem nenašla..Proto vás prosím a žádám, věděl by si někdo rady s tímhle? :(

Pravidelný komolý čtyřboký jehlan má podstavné hrany délek 6cm a 4cm. Boční stěna svírá s rovinou podstavy úhel 60°. Vypočítejte objem a povrch komolého jehlanu.

Diamanticek1 · 28. 03. 2013 12:30

↑ ((:-)): Kreslila jsem si obrázek, ale nedokážu si ten řež představit. Nevidím tam žádný trojúhelník bohužel.

Diamanticek1 · 28. 03. 2013 12:45

↑ ((:-)): Lze počítat přes trojúhelník AEC? Znám rozměr AE=3cm (polovina AB=6cm), i úhel CAE=60°, ale jak zjistím rozměr CE?

Diamanticek1 · 28. 03. 2013 12:51

↑ Diamanticek1: Až zjistím výšku pro výpočet objemu i povrchu, můžu použít tyto vzorce?
objem- $V=\frac{v}{3}(S_{1}+\sqrt{S_{1}S_{2}}+S_{2})$ a pro povrch- $S=S_{1}+S_{2}+S_{pl}$ . Domnívám se správně, když $S_{1}$ vypočítám obě podstavy jako obsah čtverce $a^{2}$ ? Tedy $S_{1}=6^{2}$ a $S_{2}=4^{2}$ ? Jak pak zjistím $S_{pl}$ do vzorečku pro výpočet povrchu jehlanu?

Diamanticek1 · 28. 03. 2013 14:11

↑ ((:-)): Asi na to jdu špatně, když bych chtěla vypočítat obsah lichoběžníku, že? Stejně neznám právě tu výšku.. Ale nic mě jinak nenapadá. Jak jste předtím psala, že mám použít fci tangens, přes jaký trojúhelník to vypočítám, když znám jen jeden rozměr a úhel 60°?

Diamanticek1 · 28. 03. 2013 14:36

↑ ((:-)): Asi jsem slepá a nemyslí mi to, ale nevím, jak zjistit ten druhý rozměr. Nebo ho není potřeba? Poslední úhel v trojúhelníku AEV je 30°, známe tedy všechny tři jeho úhly a jeden rozměr AE=3cm, druhou odvěsnu (výšku) lze vypočítat taky, když právě výška EF má být celkovým výsledkem, který neznám?

Diamanticek1 · 28. 03. 2013 15:12

↑ ((:-)):
z trojúhelníku AEV => tg 60°= $\frac{a}{3}$ -> a=tg 60° * 3 = 5,196cm
z trojúhelníku CVF => tg 60° $\frac{c}{2}$ -> c=tg 60° * 2 = 3,464cm
rozdíl výšek => 5,196-3,464=1,732cm = výsledek výšky
Myslíte, že to mám vypočítané dobře? Pak už stačí použít tyto vzorečky, když znám výšku?
objem- $V=\frac{v}{3}(S_{1}+\sqrt{S_{1}S_{2}}+S_{2})$ a pro povrch- $S=S_{1}+S_{2}+S_{pl}$ .
Obě podstavy $S_{1}$ a $S_{2}$ můžu vypočítat jako obsah čtverce $a^{2}$ ? Tedy $S_{1}=6^{2}$ a $S_{2}=4^{2}$ ? A jak pak zjistím $S_{pl}$ do vzorečku pro výpočet povrchu jehlanu?

Rumburak · 28. 03. 2013 16:53

↑ Diamanticek1:
Zdravím také.

Pravidelný komolý čtyřboký jehlan má podstavné hrany délek 6cm a 4cm. Boční stěna svírá s rovinou podstavy úhel 60°. Vypočítejte objem a povrch komolého jehlanu.

Úlohy tohoto typu lze s výhodou řešit pomocí podobnosti těles.

Komolý jehlan vznikne shruba řečeno tak, že vezmeme jehlan a "odřízneme" mu "špičku" - což je menší jehlan podobný jehlanu prvnímu,
kterému budeme říkat větší jehlan.

Začneme tím "odříznutým" jehlanem, který má podstavnou hranu $a = 4$ [cm], pro jeho výšku $v$ platí $\frac{2v}{a} = \mathrm{tg}\, 60^{\circ} = \sqrt{3}$ .
Obsah jeho podstavy je $P_1 = a^2$ , pobočné stěny $S_1 = \frac{1}{2}as$ , kde $s=\sqrt{$\frac{a}{2}$^2 + v^2}$ (výška stěny vzhledem k základně $a$ ),
objem jehlanu bude $V_1 = \frac{1}{3}P_1v$ .

Větší jehlan s podstavnou hranou $b = 6$ [cm] je podobný menšímu jehlanu v poměru $k = \frac{b}{a}$ . Odtud:

1) pro objem 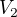$V_2$ většího jehlanu platí $V_2 = k^3V_1$ , takže objem komolého jehlanu je $V_2 - V_1 = (k^3 - 1)V_1$ .

2) pro obsah 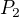$P_2$ podstavy a $S_2$ pobočné stěny většího jehlanu platí $P_2 = k^2P_1$ , $S_2 = k^2S_1$ ,

povrch komolého jehlanu tedy bude

$P_2 + P_1 + 4(S_2-S_1) = (k^2 + 1) P_1 + 4(k^2-1) S_1$ .