Matematické Fórum

↑ xstudentíkx:
to decko... nebude tam jako interval?? -nekonecna do -4 ktera tam nepatri a od -4 ktera tam nepatri do +nekonecna??

ahoj, k tomu A)
Je to kvadratická funkce kde vzorec je  y= ax^2   + bx + c

Můžou být i záporné hodnoty, protože mínus nadruhou je plus. Nemůže být -2  ani 2 protože by to bylo rovno nule.

B) záporných hodnot nenabývá podle mě, ale nejsem si jistý. Takže je prázdná množina.

C) máš dobře. Zkus ty trojky dosadit do vzorce a uvidíš ;)

D) taky asi prázdná množina

E) nevím-

Nejsem si jist, zda to mám dobře- toto jsme ve škole nikdy moc nebrali, tak to ber s rezervou

napiš správné výsledky. Možná díky nim ti napíšu správné postupy

je to rovnice pro kvadratickou fuknci. Pro lineární máš   y= ax . b  a tady más toto. Za to a b c si dosazuju jedničky, ale  příjde mi, že to asi nebude dobře. Chtělo by to, aby se ozval někdo, kdo tomu rozumí :)

C nemůže být interval, ale množina bodů -2;2. Hodnota nula je jen když ten graf funkce protíná osu x. Závorky máš správné, ale mluvíš o něčem jiném. pro množiny a pro uzavřené intervaly.
D - vše až na bod 0, kdy je funkční hodnota -4 je větší než -4. Vše až na x=0 je větší než -4. Jde tedy o sjednocení dvou intervalů tak jak máš výsledek (vše až na 0 je větší než -4).
E - když uděláš kolmici na osu y v bodě 5 a z průsečíku uděláš opět kolmici na osu x, tak ti to tu osu prostne v určitém bodě. To je bod (řekněme X), kdy se funkční hodnota rovná číslu 5. To samé na druhé straně (Y) a všechny hodnoty mezi těmito dvěmi body jsou menší než 5 -> . Zde je to konkrétně jak vidím .

Pak jsem si nemohl nevšimnout, že v intervalu mezi hodnotama píšeš čárku. Správně tam má být středník (;). Je to tam všude, kde jde o nějakou ředu čísel (zvlášť v množině to dělá bordel
)

D - tady se hodnota pod -4 nedostane, nejnižší hodnota je -4 jenv jednom bodě, v bodě 0. Všechny ostatní hodnoty jsou vyšší než -4 a ty přece hledáš. Interval všech čísel je , když z tohoto intervalu potřebuješ vyloučit jedno číslo, tak hledáš dva intervaly, které obsahují všechny čísla až na to jedno . První interval obsahuje všechny menší čísla než x (samotné x už neobsahuje) a druhý interval obsahuje všechny čísla větší než x (opět x už neobsahuje). Tak vyloučíš z intervalu všech čísel jedno - jako v tomto případě .

E - aby jsi našla přesně ten bod, kdy je funkční hodnota 5, tak to musíš rýsovat, ale často jsou u takových úloh pomocné linky, kde je to vidět. Zde je tedyhodnota 5 v bodě -3 a 3. Všechny body mezi nimi jsou menší než 5 - hodnota, kterou hledáš. Ty body mají hodnotu 5 () a tak je nutné je z intervalu vyloučit tak, že z uzavřeného intervalu uděláš otevřený interval. Platí .

Je to jasnější? :)

A jinak taky zdravim :)

E: představ si, že všechny otazníky jsou znak nekonečna :D, nevim kde tu ten znak nekonečna je a místo toho mi to udělalo tohle.

Sestavení rovnice je druhá možnost. Nedříve jsem taky nechápal na co se nás učitelka ptá, ale pak jak se do toho dostanete, tak zjistíte, jak je to jednoduchá látka :)

Jak kdy. Když to vidíš na grafu, tak se s tím dá rozumně pracovat, hodně jde vyčíst z prvního pohledu. Jsou ale taky úlohy kdy je jednodušší si sestavit rovnici a počítat. Jde obojí, záleží, co ti víc vyhovuje. Já osobně jsem přes geometrii, ale u funkcí to řeším často jen náčrkem, pak přichází počty a nakonec rýsování (sem línej rýsovat :D). Každopádně umět by jsi měla obojí, nikdy nevíš, co za příklad dostaneš.

xstudentíkx napsal(a):

Prostě pokud uvidím graf, tak si udělám rovnici a podle toho už dosadím čísla ( já to v té rovnici už jasně vidím, takže by mi to mělo jít snadněji).

Tohle mi nepřijde moc jako dobrý nápad. Snadnější to totiž není, a navíc u téhle úlohy máš zjednodušenou práci tím, že v zadání je (asi) parabola. Ale ten obrázek mohl vypadat taky třeba takhle. Velmi pochybuju, že by se ti povedlo ten funkční předpis uhádnout, a i kdyby, nemyslím že bys z něj našla to co potřebuješ.

Z toho obrázku se to ale dá vykoukat jednoduše, a jako "třídní génius" ho musíš snadno pochopit. Jinak v podstatě nechápeš co jsou funkce, a bez toho ti další studium půjde špatně. Jde o tohle. Funkce je zvíře, kterému když hodíš číslo, tak ho sežere a vypadne z něj nějaké jiné. Do grafu se to zakreslí prostě tak, že se udělá bod na souřadnicích (vstup,výstup). Pokud tedy chceš zjistit co z toho zvířete vypadne, když mu hodíš číslo 8, tak si na vodorovné ose najdeš osmičku, a podíváš se nahoru a dolů kde je graf funkce. Až ho najdeš, podíváš se jakou "výšku" v tom místě má - a to je to číslo které z funkce vypadne, když sežere osmičku.

Tvoje úloha je de facto opačná. Pokud chtějí vědět pro jaká x (vstupy) funkce vrací kladná čísla, tak se neptají na nic jiného než na x-ové (vodorovné) hodnoty takové, pro které je graf funkce nad vodorovnou osou.

↑ xstudentíkx:
To je celkem dobrá otázka, pokud ji myslíš tak jak jsem ji pochopil. Pokud se někdo ptá jakých hodnot funkce nabývá, tak tím myslí to co z té funkce leze, ne naopak. Otázka jako "pro jaká y funkce nabývá x=5" takhle nedává úplně smysl. Muselo by to být naopak, tedy "jakou hodnotu funkce nabývá pro x=5".

Ovšem narážíme tady na jednu důležitou vlastnost funkce. To naše zvíře má totiž tu vlastnost, že pro jednu pevnou hodnotu vrátí vždy stejný výsledek, a vždycky právě jeden. Pokud to nějaký obrázek nebude splňovat, a graf se bude někde "vracet", pak to není graf funkce. Jinak řečeno, když na tom obrázku budu dělat svislé čáry, tak každá čára protne graf funkce maximálně jednou.
Naopak to ale neplatí. Z toho zvířete může vypadnout stejný bobek pro více různých vstupů. To je vidět na té + a - trojce - v obou případech vypadne pětka. To není nic proti ničemu, to funkce může dělat (pak se řekne, že není prostá, ale pořád je to funkce).

To co píšeš a na co se přesně ptáš souvisí s pojmem inverzní funkce k nějaké funkci. Inverzní funkce je taková funkce, která dělá opačnou operaci k té původní. Takže nějaké funkci hodím trojku, ona mi vrátí pětku. Já tu pětku vezmu, zavolám si funkci inverzní a tu pětku jí dám sežrat. Vypadne mi zas ta trojka. Inverzní funkci ale jde sestrojit jen k prostým funkcím (které pro žádná dvě čísla nedají stejný výsledek). Kdyby funkce nebyla prostá, jako třeba ta naše, tak ta inverzní funkce by neměla jak poznat, které číslo má vrátit (v našem případě + nebo - trojku, přesně tak jak píšeš). Proto naše funkce nemá inverzní funkci, protože vyplivnout dvě čísla nesmí. Tohle asi budete teprve brát.

Příklad.. Takže třeba k funkci 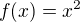inverzní funkce neexistuje. Kdybys ale levou půlku té paraboly usekla, tak už ten zbytek prostý bude a invertovat půjde. Tím vznikne druhá odmocnina, která je v jistém smyslu k té mocnině inverzní. Ale ne úplně. Třeba - to je ok (hodil jsem mocnině trojku, ta mi vrátila devítku, tu jsem hodil odmocnině, ona mi vrátila zase trojku), ale - to už ok není, protože odmocnina vrátila zase trojku, i když jsem dovnitř hodil -3ku.

No, nějak se rozepisuju, tak toho radši nechám, aby ses pak ve škole nenudila. Za chvíli začnu psát co je složená funkce, a kdoví kam by to až došlo.