Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 05. 2013 11:52 — Editoval PL4 (29. 05. 2013 12:13)
Průběh funkce
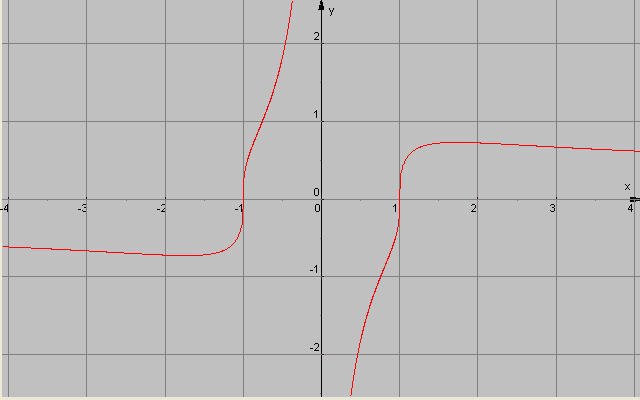
Zdravím. Pokouším se vyšetřit průběh téhle funkce: ![kopírovat do textarea $\sqrt[3]{\frac{1}{x}-\frac{1}{x^{3}}}$](/mathtex/e6/e66f41f40ec3e8c68b2080ac57e658d7.gif) . Zkusila jsem použít nějaký program na kreslení grafů (moje první setkání s takovým programem) a vůbec nevím, jak s tím pracovat. Vyšlo mi tohle: http://www.wolframalpha.com/input/?i=%2 … p;a=^_Real . Nedá se z toho programu dostat i nějaký postup, nebo alespoň náčrt? Protože ať se snažím jak chci, nemůžu se k tomuhle grafu dohrabat.
. Zkusila jsem použít nějaký program na kreslení grafů (moje první setkání s takovým programem) a vůbec nevím, jak s tím pracovat. Vyšlo mi tohle: http://www.wolframalpha.com/input/?i=%2 … p;a=^_Real . Nedá se z toho programu dostat i nějaký postup, nebo alespoň náčrt? Protože ať se snažím jak chci, nemůžu se k tomuhle grafu dohrabat.
Offline
- (téma jako vyřešené označil(a) PL4)
#2 29. 05. 2013 12:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh funkce
Zdravím,
ve WA je "problém" s 3. odmocninou, jelikož je jinak definována - podrobně. Zkus překontrolovavat pomocí MAW, případně využit zde sekci podpory. Děkuji.
Offline
#3 29. 05. 2013 12:31 — Editoval PL4 (29. 05. 2013 12:32)
Re: Průběh funkce
↑ jelena: Maw jsem zkoušela jako první, ale ten mi nějak nešel použít. Tvrdil něco v tom smyslu, že graf nevznikl transformací grafu elementrání funkce, nebo něco podobného. Asi to tam špatně zadávám, nebo tak. Zkusím to přesunout do té části na pomoc s programy. Moc děkuju za pomoc, já na tyhle věci vůbec nejsem.
Offline
#4 29. 05. 2013 14:29
Re: Průběh funkce
↑ PL4:
Ten graf (vykreslení funkce) ve tvém odkazu je dobře.
Podle mne má funkce maximum v bodě sqrt(3), minimum v bodě -sqrt(3).
Inflexní body v -6.8423, -1, -0.6576, 0.6576, 1, 6.8423.
Asymptoty bez směrnice
Pro x->0- y= oo, pro x->0+ = -oo. (x=0)
Asymptota
Pro x->+-oo y=0
Jinak to je pěkně vykutálená funkce
Offline
#5 29. 05. 2013 17:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh funkce
↑ Honzc:
Zdravím,
já neříkám, že špatně (teď nevím, zda kolegyňka ještě editovala vložení, že se volí "reálná" varianta grafu, jelikož, když jsem psala, tak mně se zobrazovala varianta komplexní). Bohužel, ve využití WA jsme narazili na více momentů s odlišnou definici (nebo s kreslením s využitím i komplexního oboru), což mate.
MAW v tomto případě také není ideální, protože nepodchycuje hodnoty, ve kterých 1. a 2. derivace neexistuje (x=1, x=-1) a neupozorňuje, že vyšetřuje pouze na polovině def. oboru. Ovšem MAW máme více v dosahu :-) a můžeme tuto záležitost prokonzultovat přímo u zdroje.
Zajímavé, že místní "Graph" vykresluje s hrotem u x=1, WA v zápisu se signum (dle doporučení k zápisu 3. odmocniny) vykresluje snad jednoznačně.
Jinak to je pěkně vykutálená funkce
:-) tak to bych neřekla - bez vyšetření (jen po stanovení def. oboru a že je lichá) se dají nakreslit 2 hyperboly, jejich rozdíl a 3. odmocnina výsledku - až bude pouť.
Offline
#6 30. 05. 2013 06:32 — Editoval Honzc (30. 05. 2013 06:37)
Re: Průběh funkce
↑ jelena:
Zdravím,
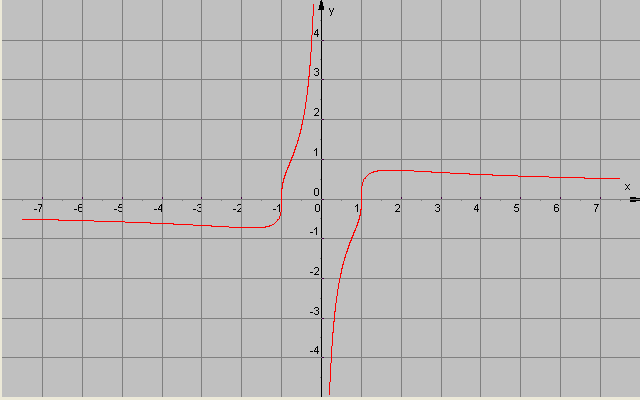
větou "Jinak to je pěkně vykutálená funkce" jsem chtěl pouze říct, že při podrobném vyšetření průběhu funkce, dělat druhou derivaci (a notabene třetí) je "pěkné" počítání - samozřejmě, že se na to dá využít i WA.
Graf (průběh) vypadá takto:
Offline
#7 30. 05. 2013 09:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh funkce
↑ Honzc:
to ano, pomohlo by zavést substituci, např.  a pracovat jako se složenou funkci (také co nejvíce využívat přepisy zlomků na součiny). Ještě jsem zkoušela vložit do programu Graph, také v pořádku kreslí.
a pracovat jako se složenou funkci (také co nejvíce využívat přepisy zlomků na součiny). Ještě jsem zkoušela vložit do programu Graph, také v pořádku kreslí.
Ale - když to porovnám s požadavky ostatních (v reálu), tak je toto procházka růžovým sadem (nebo ještě lépe městem v dešti nebo sněhu - ach :-)) Pohodový den.
Offline
#8 30. 05. 2013 10:02
Re: Průběh funkce
Moc děkuju za všechny reakce. A s tou editací mého příspěvku máte pravdu, to se omlouvám, ještě jsem si po napsání s tím programem hrála a přišla na tohle přepnutí. Jinak s tím, že je vykutálená rozhodně souhlasím, já měla v písemce řešit její průběh a nadšená jsem z toho nebyla. Ani moc úspěšná :), takže musím trénovat a tyhle programy vypadají fakt dobře, tak ještě jednou díky za pomoc s nimi.
Offline