Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
#1 03. 07. 2013 15:39 — Editoval basttien (03. 07. 2013 15:48)
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Dobrý den,
v rámci své diplom. práce bych potřeboval poradit se vzorcem, který se týká výpočtu příbuzné rozmanitosti exportu.
kde Hr = 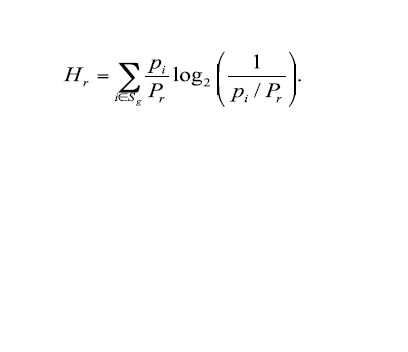
pi = podíl daného produktu na celkovém exportu
Pr = suma pi
Nerozumím tomu, jak je možné, že v některých případech, když dosadím menší pi, vyjde větší číslo, než když dosadím menší pi. Např. když jsem do vzorce dosadil pi = 0,000122 a Pr = 0,001456 vyšlo Hr = 0,09, když jsem dosadil pi = 0,000001265 a Pr = 0,001456, vyšlo Hr = 0,0027, což mi přijde logické, čím větší pi dosadím, tím větší Pr vyjde. Když jsem ale dosadil pi = 0,001028 a Pr = 0,001456 vyšlo Hr = 0,107, když jsem však dosadil pi = 0,0002197 a Pr = 0,001456 vyšlo Hr = 0,12 čili vyšel vyšší výsledek než u dosazení většího pi. Chtěl bych se zeptat, jestli by mi někdo mohl poradit, resp. vysvětlit, jak je toto možné?
Děkuji za rady
Offline
- (téma jako nevyřešené označil(a) jelena)
#2 03. 07. 2013 18:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Zdravím,
vzorec a problematiku neznám, nevím, jak kolegové (pokud bys měl podrobnější odkaz, na co se mám(e) podívat), určitě by to prospělo.
Zatím se dívám na to, co je v příspěvku ↑ basttien:. Moje otázky:
a) proč je ve vzorci 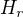 znak sumy? Počítáš za jeden (i-ty) produkt, nebo se to ještě sčítá za více produktů?
znak sumy? Počítáš za jeden (i-ty) produkt, nebo se to ještě sčítá za více produktů?
b)
pi = podíl daného produktu na celkovém exportu
Pr = suma pi
je to poměrově (jako "hmotnostní zlomek" např.)? (může nabývat jak p_i, tak Pr jen hodnot od 0 do 1)?
c) když zkusím zadat Hr jako funkci 2 proměnných (pi=x, Pr=y) za předpokladu, že bez sumy, pouze pro jeden pi, potom funkce vykazuje extrém (alespoň dle WA). Tedy pokud se pohybuješ jednou před a potom po extrému, tak je možné takové pozorování (ale chtělo by to znát vazbu mezi pi a Pr, jelikož teď hodnota Pr je mimo mnou předpokládaný interval).
Je teoretický (praxe?) předpoklad, že Hr má extrém? Děkuji za upřesnění.
Offline
#3 03. 07. 2013 20:02
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Děkuji Vám za odpověď,
zkusím postup výpočtu upřesnit. Jelikož ale nejsem matematik, tak moje vysvětlení nebude zrovna fundované. "pi" je podíl dané exportní komodity na celkovém exportu, tzn. např. komodita "strojní zařízení" vykazovala hodnotu 604 405 000 Kč, celkový export činil v daném roce 93 136 000 000 Kč, podíl komodity je tedy 604 405 000/ 93 136 000 000 = 0,006489. "Pr" představuje exportní sekci, kam spadají všechny příslušné komodity - čili "Pr" je suma "pi". Samotný výpočet jsem pak provedl tak, že jsem do vzorce pro výpočet Hr dosazoval příslušné hodnoty pi a Pr....když jsem získal hodnoty Hr pro každou exportní sekci, dosadil jsem hodnoty Hr do vzorce pro výpočet Related Variety (Suma Pr x Hr) a to tak, že jsem provedl výpočet pro každou sekci zvlášť....tzn. Pr (1. exportní sekce) x Hr (1. exportní sekce) + Pr (2.exportní sekce) x Hr (2.exportní sekce)..........= celkový výsledek
Doufám, že moje vysvětlení dává alespoň trochu smysl
Děkuji vám za ochotu
↑ jelena:
Offline
#4 03. 07. 2013 22:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
↑ basttien:
děkuji za vysvětlení, skoro jasné, jen tomu nerozumím:
"Pr" představuje exportní sekci, kam spadají všechny příslušné komodity - čili "Pr" je suma "pi"
Pr by se rovnala 1, pokud bychom počítali pi pro každou komoditu, která se podílela na exportu (i tu s nejmenším, skoro zanedbatelným, přínosem), ovšem jak zde čtu (str. 7 a okolo nebo 9 v pdf), v tomto výpočtu si vybírají komodity s významným postavením? Rozumím tomu dobře?
Bylo by možné ještě ukázat (vysvětlit) výpočet pro více komodit a co si mám představit pod 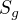 (viz v odkazu). Je prováděn nějaký výběr dle významnosti podílu sektoru na exportu, podle kterého kritéria? Děkuji.
(viz v odkazu). Je prováděn nějaký výběr dle významnosti podílu sektoru na exportu, podle kterého kritéria? Děkuji.
Jelikož ale nejsem matematik
:-) také tak.
Offline
#5 03. 07. 2013 23:11
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Ano, máte pravdu,
v ideálním případě by suma měla dávat 1, bohužel co se týče dat za export, tak většinou nejsou data úplná, takže suma všech komodit většinou nedává 1. Nevybírají se komodity, které by byly nějak významné, ale počítá se s těmi komoditami, jejichž data jsou k dispozici. Suma Sg znamená (alespoň tedy doufám) počet exportních sekcí.
Děkuji Vám
↑ jelena:
Offline
#6 04. 07. 2013 00:10
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
zde ještě s dovolením uvádím dílčí část mých výpočtů (výpočty prováděny v excelu)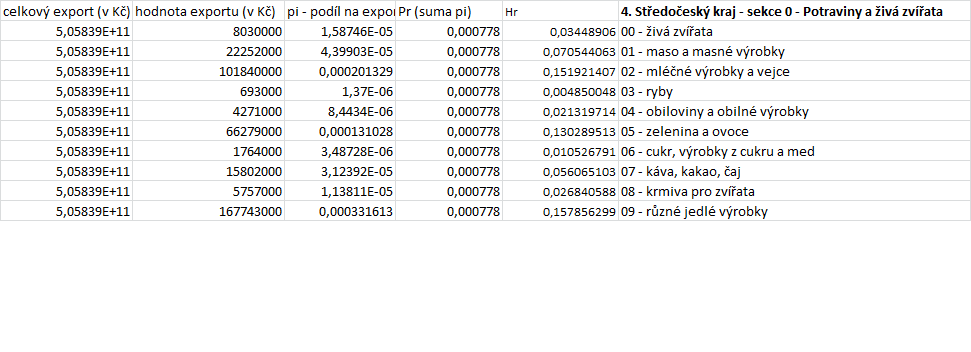
Děkuji Vám
↑ basttien:
Offline
#7 04. 07. 2013 00:50
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
zde pak ještě s dovolením uvádím příklad výsledků, kde vyšší hodnota dosazeného "pi" neznamenalo vyšší výsledek, ale paradoxně menší výsledek Tyto výsledky (Hr) jsem zvýraznil tučnou kurzivou.
Děkuji Vám
↑ basttien:
Offline
#8 04. 07. 2013 07:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Děkuji za další upřesnění a za data.
bohužel co se týče dat za export, tak většinou nejsou data úplná, takže suma všech komodit většinou nedává 1.
to se mi nezdá - pokud jsou chybějící data, ale máme celkový součet za export, tak se dá vyznačit položka "ostatní".
Potom, pokud se dívám na indexy pro sumy (jednou to jsou i - pro  a
a 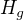 a
a 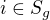 , potom ale index g, přičemž g je od 1 do G - pro RV).
, potom ale index g, přičemž g je od 1 do G - pro RV).
A já mám takový dojem z materiálů, že pokud nečleníme na další skupiny dat, tak v jednom výpočtu máme p1, p2, p3....pn podle podílu komodit, po sečtení těchto pi dostaneme jen jednu hodnotu  . A také dosazováním do vzorce
. A také dosazováním do vzorce  dostaneme jen jednu hodnotu
dostaneme jen jednu hodnotu 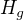 . Násobením těchto hodnot dostaneme jednu hodnotu RV, jelikož nemáme přes co sčítat přes index g).
. Násobením těchto hodnot dostaneme jednu hodnotu RV, jelikož nemáme přes co sčítat přes index g).
Mohla bych ještě vidět vzorec (přímo zápis do EXCEL) pro výpočet pro sloupec 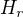 v jednotlivých tabulkách, co jste přidal do posledních 2 příspěvků)? Nějak se mi nezdá, že by výsledky v tabulce odpovídaly tomuto postupu:
v jednotlivých tabulkách, co jste přidal do posledních 2 příspěvků)? Nějak se mi nezdá, že by výsledky v tabulce odpovídaly tomuto postupu:
Samotný výpočet jsem pak provedl tak, že jsem do vzorce pro výpočet Hr dosazoval příslušné hodnoty pi a Pr...
Děkuji.
Offline
#9 04. 07. 2013 11:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Přidám ještě takovou výzvu pro kolegy, pokud by se někomu chtělo v problému angažovat matematicky.
Teorie ke čtení je v odkazech: Odkaz1 a Odkaz2. Jednotlivé členy "problematického" výpočtu  jsem zkoušela z dat kolegy ↑ basttien: počítat v EXCEL (a ještě jsem pár dat v rozmezí celého exportu přidala).
jsem zkoušela z dat kolegy ↑ basttien: počítat v EXCEL (a ještě jsem pár dat v rozmezí celého exportu přidala).
Zdá se, že tvar 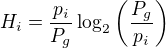 má do do činění s log-normálním rozdělením (tedy výskyt maximu, který kolegu zaskočil, je možný). Také problém má co do činění s entropii. Možná někoho z vás problém osloví, budu vděčná.
má do do činění s log-normálním rozdělením (tedy výskyt maximu, který kolegu zaskočil, je možný). Také problém má co do činění s entropii. Možná někoho z vás problém osloví, budu vděčná.
Offline
#10 04. 07. 2013 11:18
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Dobrý den,
vzorec pro výpočet Hr v Excelu jsem definoval následovně: Hr = LOG ((1/ ( pi/Pr )) * (pi/Pr), takže konkrétně s čísly vypadá zápis následovně: LOG ((1/(0,000219737/0,001456) * (0,000219737/0,001456) = 0,1239. Doufám, že nevadí, že napřed vypočtu logaritmus závorky LOG ((1/(pi/Pr)) a pak toto číslo vynásobím číslem v závorce tj. * (pi/Pr)
Děkuji Vám
↑ jelena:
Offline
#12 04. 07. 2013 11:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
↑ basttien:
děkuji, výpočet dle uvedeného zápisu je v pořádku pro dekadický logaritmus (jen ještě pozor na závorky) - výsledek souhlasí, ale dle vzorce má být základ log_2, výsledek tak, ještě třeba opravit v EXCEL.
Ovšem toto je jen drobná oprava. Jak jsem psala v předchozím příspěvku, mně vychází, že "vývoj dat" může mít maximum na křivce Hr. To bychom asi nakonec zdůvodnili. Jen zbývá si udělat jasno se závěrem výpočtu RV (přes co je sumace, pokud vůbec?).
ještě bych počkala i na názory kolegů k problému. Hoří to moc? :-)
Offline
#13 04. 07. 2013 11:50
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Zde uvádím odkaz na článek v pdf, ze kterého jsem čerpal já. - Boschma et al., 2010. Vzorec je na straně 10.
http://paginaspersonales.deusto.es/amin … eg1012.pdf
Děkuji Vám
↑ basttien:
Offline
#14 04. 07. 2013 12:04
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Moc Vám děkuji,
takže jestli tomu dobře rozumím log 2 není dekadický logaritmus? Já si myslel, že log 2 je jiný zápis pro dekadický logaritmus. Prosím, je mi to trapné, ale mohla byste mi poradit, kde v excelu najdu funkci log 2? Já v excelu našel pouze funkci log. Co se týče sumace Hr a výpočtu samotné RV, tak jsem váhal, jestli je správné a) vypočítat RV pro každou exportní sekci, tzn. Pr x Hr pro každou sekci a pak tyto dílčí výsledky sečíst nebo b) udělat sumu všech Hr a Pr napříč sekcemi a pak tyto výsledná čísla vynásobit mezi sebou. Osobně si myslím, že asi lepší je varianta a. Diplmoku mám odevzdat v 21. srpna, takže čas je :).Děkuji Vám za ochotu, díky Vám už tuto problematiku začínám lépe chápat, alespoň doufám.
Hezký den
↑ basttien:
Offline
#15 04. 07. 2013 16:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
↑ basttien:
děkuji, odkazovaný materiál zkusím prohlédnout podrobněji (v kapitole "Variete indexes" hned na úvod píší o seskupení komodit dle takového třídění?). Nejsou to uskupení, co diskutujeme?
kde v excelu najdu funkci log 2
log_2 oproti dekadickému má základ 2, v EXCEL pohledat "Matematické funkce" a zvolit LOGZ, v závorce na 1. pozicí bude podíl buněk, co počítáme, na 2. pozici bude 2 - jako základ log).
už tuto problematiku začínám lépe chápat, alespoň doufám.
:-) teď abych to začala chápat ještě i já. Ale času do srpna je dost. Nestalo by za to se zeptat vedoucího ohledně seskupení do tříd a použití vzorců? Bylo by to jistější (jinak k samotnému původnímu problému tématu "jak je možné, že v některých případech, když dosadím menší pi, vyjde větší číslo, než když dosadím menší pi." to bych řekla, že funkce se tak chová, že vykazuje maximum).
Offline
#16 04. 07. 2013 17:08
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Máte pravdu,
třídění dle HS (Harmonized system) je jedním z možných třídění komodit do tříd. Já používám třídění dle SITC 2- základní tabulka tříd obsahuje 10 tříd (0 až 9)...zde je odkaz....http://www.czso.cz/csu/2012edicniplan.nsf/t/AD002CF78A/$File/60011209j02_c.pdf Já počítám se třídami na úrovni agregace SITC 2, to znamená, že každá z těchto tříd obsahuje dílčí komodity. Hned jdu zkusit přepočítat výsledky. Pak zde s dovolením uveřejním výsledky, ke kterým jsem přišel
Děkuji Vám za ochotu
↑ jelena:
Offline
#17 05. 07. 2013 10:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
↑ basttien:
děkuji, již v tom mám jasno. Máme úrovně třídění:
první (vyšší) dle SITC, zde budeme používat indexy  (můžeme i shodně s tříděním od 0 do 9, nebo jak udává vzorec g je od 1 do G, což je 10). V článku je zde označení indexu _r.
(můžeme i shodně s tříděním od 0 do 9, nebo jak udává vzorec g je od 1 do G, což je 10). V článku je zde označení indexu _r.
Každá třída se ještě člení na sekce - příklad členění sekce 0 ↑ příspěvek 7:. To je druhé (nižší) třídění, zde pro každou sekci používáme "vnitřní" indexy i.
Pro jednotlivé sekce vypočteme  - je to součet ve sloupci "
- je to součet ve sloupci " " a
" a 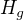 - je to součet ve sloupci
- je to součet ve sloupci 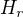 . Budeme mít 10 hodnot
. Budeme mít 10 hodnot  a k nim odpovídající
a k nim odpovídající 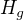 , což použijeme do vzorce
, což použijeme do vzorce  .
.
Ohledně "nevysvětleného chování" jednotlivých H_i - to jsme si řekli, pro příklad z příspěvku 7 (doplnila jsem pro názornost pár hodnot z povoleného intervalu) funkce H_i může mít takový tvar.
Ještě obecně ke zpracování "chybějící data". Pokud znám celkovou hodnotu exportu a hodnoty exportů za jednotlivé třídy dle členění SITC, potom chybějící data v podsekcích podrobného třídění (káva, ryby) bych doplnila dopočtem do položky "09-různé jedlé výrobky". To proto, že součet p_i za sekci musí dávat P_g podíl sekce na celkovém exportu a tento podíl je znám (můžeme vypočíst jako "export třídy dle SITC"/"celkový export"). Jinak to k sobě sedět nebude a nebude udávat správně váhy. V komentáři pro zpracování dat bych to tak zdůvodnila.
Mně nejvíce jasno udělal tento článek. Zdárnou práci přeji.
Offline
#18 05. 07. 2013 12:39
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Dobrý den,
moc Vám děkuji. Snad poslední dotaz, za každou sekci dostanu jedno číslo Pg (což je součet daných komodit pi) a jedno číslo Hg (což je součet Hr), na konkrétním příkladu Středočeského kraje, (příspěvek č. 6 -jen pro ilustraci, výsledky zmíněné v příspěvku 6 jsou počítány ještě se špatným dekadickým logaritmem) by tedy výsledek vypadal následovně...Pg = součet komodit tzn. 0,00001587 (živá zvířata) + 0,00004399 (maso a masné výrobky)....
= 0,000778 a součet Hr = 0,0345 (živá zvířata) + 0,0705 (maso a masné výrobky)...takže by se RV = 0,000778 * 0,6647 = 0,00005171
Nebo je správně že Pg by měla být suma ve sloupci Pr, tzn. 0,000778 + 0,000778.....= 0,00778, takže výsledek za sekci by byl RV = Pg *Hg = 0,00778 *0,6647 = 0,005171
Doufám, že jsem to popsal srozumitelně
Děkuji Vám
↑ jelena:
Offline
#19 05. 07. 2013 14:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Pg = součet komodit tzn. 0,00001587 (živá zvířata) + 0,00004399 (maso a masné výrobky)....
= 0,000778 a součet Hr = 0,0345 (živá zvířata) + 0,0705 (maso a masné výrobky)...takže by se RV_(prvni sekce do součtu) = 0,000778 * 0,6647 = 0,00005171
Ano, za jednotlivou sekci máme mít pouze součet sloupece  a součet pod sloupcem
a součet pod sloupcem 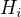 (sekce jsme očíslování indexem g=1 až g=10), tedy sekce 0 "potraviny" bude mít index g=1. V samotné sekci "0 Potraviny" jsme součtem dostali:
(sekce jsme očíslování indexem g=1 až g=10), tedy sekce 0 "potraviny" bude mít index g=1. V samotné sekci "0 Potraviny" jsme součtem dostali: 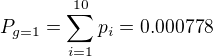
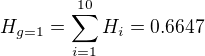
Ve vzorci RV se objeví součet takových násobků za každou sekci: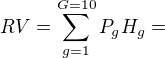
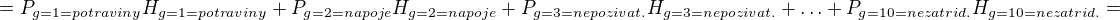
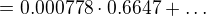
Offline
#21 05. 07. 2013 16:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
↑ basttien:
také děkuji a úspěšné dokončení práce (ještě bych doporučovala chybějící data probrat s vedoucím - jelikož součet P_g už musí dávat 1, nebo alespoň jaké procento chybějících dat k celkovému součtu exportu je "akceptovatelných"). Hodná určitě nejsem a třeba tento moment bych zkritizovala :-) Pohodový den.
Offline
#22 08. 07. 2013 09:09 — Editoval jelena (08. 07. 2013 19:47)
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Dobrý den,
prosím, měl bych ještě dotaz ohledně příbuzné rozmanitosti, konkrétně dotaz chybějících dat. V příspěvku č. 8 jste napsala, že
" To se mi nezdá - pokud jsou chybějící data, ale máme celkový součet za export, tak se dá vyznačit položka "ostatní". Chtěl bych se zeptat, zda-li postupuji správně, když jsem např. u chybějících dat sekce 0 - potraviny a živá zvířata udělal dopočet chybějících dat tak, že jsem na stránkách statistického úřadu zjistil export za danou sekci, od které jsem odečetl hodnoty exportu za komodity, pro které jsou data. toto číslo, které vyšlo jsem vydělil celkovým exportem, čímž jsem dostal položku "ostatní". Matematicky vyjádřeno. 4151 000 000 - 301 527 000 (součet hodnot exportu komodit, pro které jsou data) = 3849473000 - toto číslo je strašně velké, buď je chyba v počtu 0 u součtu "známých dat", nebo data se nevztahuji k sobě.
Toto číslo jsem vydělil celkovým exportem....tzn. 3849473000/207 148 000 000 = 0,01858. V ideálním případě by součet pi - podílu komodit měl dávat 1, tedy celek, rozumím tomu dobře?
Pak bych měl ještě dotaz k nepříbuzné rozmanitosti, resp. pouze ke správnosti matematického vyjádření.
Postupoval jsem podle vzorce na straně 14 v tomto dokumentu (už jsem Vám ho posílal dříve)......http://paginaspersonales.deusto.es/aminondo/Materiales_web/PIRS_July2011.pdf
Matematické vyjádření mého výpočtu je následující (v tabulce chybí poslední řádek a 60 mln.)
zápis v excelu je následující: u sekce 0 potraviny a živá zvířata: 0,020038813*LOGZ (1/0,020038813) = 0,113040128
Součet všech vypočtených hodnot nepříbuzné rozmanitosti pak činí 1,456.....tento výsledek se mi nějak nezdá, protože v práci, která toto hodnotila pro celé Česko, vycházely menší hodnoty, např. v roce 2010 byla hodnota nepříbuzné rozmanitosti 2,6934....a mně vyšla jen za Plzenksý kraj 1,456....chtěl jsemse zeptat, jestli by se toto číslo ještě nemělo vydělit 100, aby se získaly procenta....jinak nevím, proč mně vychází tak velké hodnoty...v kontextu s výsledkem 2,6934
Děkuji Vám
Hezký den
Offline
#23 08. 07. 2013 09:11
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
jen jsem ještě zapomněl dodat, že hodnota 2,6934 je za celé Česko
Děkuji
↑ basttien:
Offline
#24 08. 07. 2013 13:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
↑ basttien:
Také pozdrav,
ohledně chybějících dat. Pokud jsou data "celkový export" za celou ČR a ve výpočtech se používají data jen za Středočeský kraj, tak samozřejmě "chybějící" nehledáme. Je však správné vztahovat rozčlenění na položky za kraj k celkovému za ČR, nebo položky za kraj se mají vztahovat jen k celkovému za kraj? To je jen moje otázka.
Moje kontrola na "součet P rovný 1" by byla jen v tomto případě: "celkový export" mám za Středočeský kraj, tento export se v kraji člení na třídy dle SITC a každá tato třída se ještě člení na podsekce podrobného tříděni. Cca by "odzdola měl být součet, ale pro způsob sběru dat předpokládám nějaké "ostatní a nepodchycené".
"Nepříbuzná rozmanitost" se rozumí vzorec [mathjax]URV=\sum_{j=1}^{N}P_j\log_2(\frac{1}{P_j})[/mathjax] (to jen zkouším zápis), vzorec: 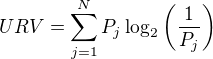 . To bych řekla, že jelikož se jedná o poměrový údaj, tak by měl odrážet jen chování systému, ne velikost systému. Snad by se mohl zapojit někdo z kolegů, kdo se orientuje v informační entropii..
. To bych řekla, že jelikož se jedná o poměrový údaj, tak by měl odrážet jen chování systému, ne velikost systému. Snad by se mohl zapojit někdo z kolegů, kdo se orientuje v informační entropii..
chtěl jsemse zeptat, jestli by se toto číslo ještě nemělo vydělit 100, aby se získaly procenta]
P jsou poměry, tedy % by vznikla vynásobením 100 :-) Ale není nutné, protože s % nepracujeme.
Offline
#25 08. 07. 2013 14:10
- basttien

- Příspěvky: 37
- Škola: UK - katedra sociální geografe a reg. rozvoje
- Pozice: student
- Reputace: 0
Re: Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)
Děkuji Vám,
já analyzuji všechny kraje Česka, takže jestli tomu dobře rozumím, když sečtu všechny Pr (sumy komodit) za všechny sekce exportu (potraviny, nápoje a tabák...) tak by toto číslo v ideální případě mělo dávat v součtu 1, neboť by to znamenalo, že byly k dispozici všechny data týkající se exportu za dané sekce. Proto např. v mém předcházejícím příspěvku jsem provedl dopočet chybějících dat, tak jak jsem naznačil...."zbytek" tzn....3849473000 Kč jež nejsou přiřazeny určité komoditě, proto jsem toto označil jako "ostatní" a provedl dopočet
...... 3849473000/207 148 000 000 = 0,01858 (pi) ....a pak vypočetl i Hr pro toto číslo....doufám, že je to tak relevantní řešení dopočtu chybějících dat, když znám kromě hodnoty celkového exportu kraje znám i hodnotu exportu tohoto odvětví pro daný kraj. Nebo by byla vhodnější varianta počítat pouze s hodnotami, jež jsou exaktně zmíněny a zbytek nedopočítávat?
U vzorce nepříbuzné rozmanitosti mi není jasné, proč vychází tak velká čísla, myslím (doufám), že zápis v excelu je v pořádku.
V této studii
http://webcache.googleusercontent.com/s … &gl=cz
vyšla max. hodnota nepříbuzné rozmanitosti 1,16....mně jen za jedno odvětví v kraji 1,456...
Děkuji za pomoc
↑ jelena:
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vzorec výpočtu Related Variety (příbuzné rozmanitosti exportu)