Matematické Fórum

↑ majoSLOVAKIA:

Jedná se o lineární diferenční rovnici prvního řádu s konstantními koeficienty a tzv. speciální pravou stranou. Pro řešení takového druhu rovnic existuje snadný obecný algoritmus, který spočívý ve vyřešení přidružené homogenní rovnice a následného určení hlavní části řešení dané diferenční rovnice, která (hlavní část) je dána pravou stranou rovnice a kořenem charakteristické rovnice.


Krok 1 (vyřešení přidružené homogenní rovnice):
==============





Krok 2 (nalezení hlavní části řešení):
==============
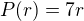Pravou stranu zapíšeme ve tvaru , kde je nějaké reálné číslo a je polynom s reálnými koeficienty v proměnné . Snadno nahlédneme, že platí a . Hlavní část řešení, označme ji třeba 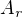, konstruujeme v následujícím tvaru takto:



kde je násobnost čísla jakožto kořenu charakteristické rovnice (jistě je 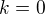, neboť ) a 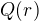je obecný polynom stejného stupně jako polynom , tedy 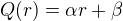, . Odtud konečně



Nyní dosadíme hlavní část řešení do původní (nehomogenní) diferenční rovnice:



Nyní porovnání koeficientů (jak je barevně označeno) dostáváme jednoduše nejprve a podobně s využitím tohoto mezivýsledku . Odtud





Krok 3 (sestavení obecného řešení původní diferenční rovnice):
==============

Řešení zadané diferenční rovnice najdeme snadno ve tvaru 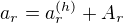, tedy




Poznámka:
(1) Co se týče partikulárního řešení, bylo by nutno znát počáteční podmínku. Protože tato není dána, není možné výpočet úlohy dokončit. Je tedy buď špatně zvolen název příspěvku nebo je zadání problému neúplné.
(2) Vzhledem k tomu, že je již po zkouškovém období na VŠB, dovolil jsem si uvést celé řešení. Snad to nebude ke škodě.