Matematické Fórum

___JIRIK___

Prosím Vás o pomoc s některými příklady, se kterými si opravdu nevím vůbec rady.

1) Kouli o poloměru R je opsán rotační kužel o výšce v. Nalezněte objem tohoto kužele.
2)Vypočítejte objem pravidelného čtyřstěnu o hraně a.
3)Vypočítejte objem pravidelného čtyřstěnu o výšce v.
4)Objem pravidelného šestibokého hranolu V = cm3. Délka podstavné hrany a je k délce výšky v v poměru 3:5. Vypočítejte povrch hranolu.
5)Do koule o poloměru r je vyvrtán otvor tvaru rovnostranného válce. V jakém poměru jsou objemy koule a válce?
6)Určete poměr obsahů trojúhelníka ABC a čtyřúhelníka TKBL, kde T je těžiště trojúhelníka ABC a K,L jsou středy úseček AB, BC.

Úloh je docela velké množství, doufám že si s tím někdo z Vás bude vedět rady. Moc děkuji ___JIRIK___

gadgetka · 07. 03. 2009 23:04

1)
$V_{koule}=\frac{4}{3}\pi{R^3}\nl3V_{koule}=4\pi{R^3}\nlR=\sqrt[3]{\frac{3V}{4\pi}}$

$R=1/3v=r==>v=3r\nl V_{kuzele}=\frac{1}{3}\pi{r^2}*v\nlV_{kuzele}=\frac{1}{3}\pi{r^2}*3r\nlV_{kuzele}=\pi{r^3}\nl$

$R=r\nlV_{kuzele}=\pi*(\sqrt[3]{\frac{3V_{koule}}{4\pi}})^3\nlV_{kuzele}=\pi*\frac{3V_{koule}}{4\pi}\nlV_{kuzele}=\frac{3}{4}*V_{koule}$

gadgetka

2)
Musíme vypočítat stěnovou výšku. Když si ve čtyřstěnu ABCD vyznačíš tělesovou výšku, je to vlastně úsečka DD', tak pro délku úsečky CD' bude platit, že je rovna 2/3 stěnové výšky. Všechny stěnové výšky v pravidelném čtyřstěnu jsou stejně dlouhé, protože stěny čtyřstěnu tvoří shodné rovnostranné trojúhelníky.

Pro stěnovou výšku x platí (z Pythagorovy věty):

$x^2=a^2-(\frac{a}{2})^2\nlx^2=a^2-(\frac{a^2}{4})\nlx^2=\frac{4a^2-a^2 }{4}\nlx^2=\frac{3a^2 }{4}==>x=\frac{a\sqrt{3}}{2}$

$\|CD'\|=\frac{2}{3}*x=\frac{2}{3}*\frac{a\sqrt{3}}{2}=\frac{a*\sqrt{3}}{3}$

Pro vyjádření délky úsečky DD' (tělesové výšky) použijeme opět Pythagorovu větu:

$\|DD'\|^2=\|CD\|^2-\|CD'\|^2\nlv^2=a^2-(\frac{a*\sqrt{3}}{3})^2\nlv^2=a^2-\frac{a^2}{3}\nlv^2=\frac{3a^2-a^2}{3}\nlv^2=\frac{2a^2}{3}\nlv=a*\sqrt{\frac{2}{3}}$

$V=\frac{1}{3}*S_p*v\nlV=\frac{1}{3}*\frac{a*x}{2}*v\nlV=\frac{1}{3}*\frac{a*\frac{a*\sqrt{3}}{3}}{2}*a*\sqrt{\frac{2}{3}}\nlV=\frac{1}{3}*\frac{a^2*\sqrt{3}}{4}*a*\sqrt{\frac{2}{3}}\nlV=\frac{a^3*\sqrt{6}}{12*\sqrt{3}}\nlV=V=\frac{a^3}{12}*\sqrt{2}(j^3)$

gadgetka · 08. 03. 2009 04:25

5)

$V_{koule}=\frac{4}{3}\pi{r^3}\nlV_{valce}=\pi*x^2*v$ x je poloměr podstavy rovnostranného válce

V rovnostranném válci platí: $v=2x$

Podle Pythagorovy věty:
$(2r)^2=(2x)^2+(2x)^2\nl4r^2=8x^2\nlr^2=2x^2==>x^2=\frac{r^2}{2}==>x=r*\frac{\sqrt{2}}{2}$

$V_{valce}=\pi*x^2*v\nlV_{valce}=\pi*(r*\frac{\sqrt{2}}{2})^2*2*r*\frac{\sqrt{2}}{2}\nlV_{valce}=\frac{\pi*4\sqrt{2}*r^3 }{8}=\frac{\sqrt{2}}{2}*\pi*r^3\nl\frac{V_k}{V_v}=\frac{\frac{4}{3}\pi*r^3}{\frac{\sqrt{2}}{2}*\pi*r^3}=\frac{8}{3\sqrt{2}}=\frac{8\sqrt{2}}{6}=\frac{4\sqrt{2}}{3}$

gadgetka · 08. 03. 2009 05:29

4)
$\frac{a}{v}=\frac{3}{5}==>v=\frac{5}{3}a\nlV=S_p*v\nlS_p=6*\frac{a*x}{2}=3ax\nlS_h=2S_p+Q=6ax+6av=6a(x+v)$

$x^2=a^2-\frac{a^2}{4}=\frac{3a^2}{4} ==>x=\frac{\sqrt{3}}{2}*a$

$V=3a*\frac{\sqrt{3}}{2}a*\frac{5}{3}a=540\sqrt{3}\nl15a^3\sqrt{3}=3240\sqrt{3}\nla^3=\frac{3240}{15}==>a=\sqrt[3]{216}=6$

$S_h=6*6(\frac{\sqrt{3}}{2}*6+\frac{5}{3}*6)=108\sqrt{3}+360\approx547cm^2$

___JIRIK___ · 08. 03. 2009 12:13

Mockrát děkuji!!! Zachránila jsi mi krk :-)

musixx · 10. 03. 2009 09:55 — Editoval musixx (10. 03. 2009 09:59)

↑ ___JIRIK___:
3)
Ve hre jsou jen rovnostranne trojuhelniky, tedy teznice, vysky a osy uhlu splyvaji a toho se da dobre vyuzit. Nejprve bych si vyjadril vysku pomoci hrany. To je jednoduche: vyska v podstave je jen vyska v rovnostrannem trojuhelniku, pak vezmu treba teziste v podstave a z nej vztycim telesovou vysku, coz mi da opet z Pythagorovy vety telesovou vysku (prepona je delka hrany, jedna odvesna jsou 2/3 teznice=vysky trojuhlenika v podstave). Pri standardnim znaceni vyjde $v=\sqrt{a^2-\left(\frac23\cdot\frac{\sqrt3}2a\right)^2}=\frac{\sqrt6}3a$ .

Pro objem si staci uvedomit, ze jde vlastne o jehlan. Takze "tretina z obsahu podstavy krat vysky". Neboli 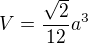$V=\frac{\sqrt2}{12}a^3$ . Tot standardni znaceni. Zrejme tez je $a=\frac3{\sqrt6}v=\frac{3\sqrt6}6v=\frac{\sqrt6}2v$ a staci uz jen dosadit.

6)
Udelal bych takovy maly podfuk a predpokladal bych, ze zadani ma smysl (tedy ze plati pro kazdy trojuhlenik). Totiz za predpokladu, ze takovy pomer existuje a nezalezi nijak na "typu" trojuhlenika ABC, pak tento pomer staci najit pro rovnostranny trojuhlenik, kde je to ovsem jasne, protoze tam vysky splyvaji s tezicemi, tedy teznice rozdeli trojuhlenik na sest stejnych trojuhleniku a dva z nich tvori onen ctyruhelnik, proto onen pomer je 6:2 = 3:1.

Matematické Fórum

#1 07. 03. 2009 17:51 — Editoval _JIRIK_ (08. 03. 2009 12:54)

Obvody, obsahy, objemy a povrchy

#2 07. 03. 2009 23:04

Re: Obvody, obsahy, objemy a povrchy

#3 08. 03. 2009 03:36 — Editoval gadgetka (08. 03. 2009 03:36)

Re: Obvody, obsahy, objemy a povrchy

#4 08. 03. 2009 04:25

Re: Obvody, obsahy, objemy a povrchy

#5 08. 03. 2009 05:29

Re: Obvody, obsahy, objemy a povrchy

#6 08. 03. 2009 12:13

Re: Obvody, obsahy, objemy a povrchy

#7 10. 03. 2009 09:55 — Editoval musixx (10. 03. 2009 09:59)

Re: Obvody, obsahy, objemy a povrchy

Zápatí

Matematické Fórum

#1 07. 03. 2009 17:51 — Editoval ___JIRIK___ (08. 03. 2009 12:54)

Obvody, obsahy, objemy a povrchy

#2 07. 03. 2009 23:04

Re: Obvody, obsahy, objemy a povrchy

#3 08. 03. 2009 03:36 — Editoval gadgetka (08. 03. 2009 03:36)

Re: Obvody, obsahy, objemy a povrchy

#4 08. 03. 2009 04:25

Re: Obvody, obsahy, objemy a povrchy

#5 08. 03. 2009 05:29

Re: Obvody, obsahy, objemy a povrchy

#6 08. 03. 2009 12:13

Re: Obvody, obsahy, objemy a povrchy

#7 10. 03. 2009 09:55 — Editoval musixx (10. 03. 2009 09:59)

Re: Obvody, obsahy, objemy a povrchy

Zápatí

#1 07. 03. 2009 17:51 — Editoval _JIRIK_ (08. 03. 2009 12:54)