Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 01. 2015 12:59 — Editoval geovektor (27. 01. 2015 13:01)
Dokaz vlasnosti
Ahojte, mam velmi specificky problem. Dostal som za ulohu dokazat vlasnosti funkcie kosinus, mam dokazat pomocou derivacie  a bolzanovej vety ze: Funkcia
a bolzanovej vety ze: Funkcia  na intervale
na intervale 
dalej ze klesa na  a ze nadobuda maximum v bodoch
a ze nadobuda maximum v bodoch  a minimum v bodoch
a minimum v bodoch  Pomozete mi s tym? Vobec neiem ako na to, viem co hovori bolzanova veta, ale ako ju vyuzit s derivaciou? Prosim aspon o navod. Budem vam vdacny.
Pomozete mi s tym? Vobec neiem ako na to, viem co hovori bolzanova veta, ale ako ju vyuzit s derivaciou? Prosim aspon o navod. Budem vam vdacny.
Offline
#2 27. 01. 2015 13:44
Re: Dokaz vlasnosti
↑ geovektor:
Ahoj.
Záleží na tom, z jakých dalších vlastností funkcí sinus , kosinus se má vycházet - teorii těchto funkcí je možno
vybudovat vícero způsoby. Dejme tomu, že o funkci sinus již víme, že
(1) nabývá kladných hodnot na intervalech  ,
,
(2) nabývá záporných hodnot na intervalech  ,
,
(3) je spojitá
(při tom předpokládáme, že  probíhá množinu všech celých čísel).
probíhá množinu všech celých čísel).
Potom z uvedených vlastností a Bolzanovy věty plyne, že sinus nabývá hodnoty 0 v krajních bodech uvedených
intervalů.
Z podmínky (1) plyne, že pro libovolné  je
je  , což dává
, což dává
informaci o chování funkce cosinus na tomto intervalu stran monotonie. Podobně dále.
Ale vše bude záviset na tom, jak jste si funkce sinus, kosinus zavedli na vaší přednášce a co už o nich máte dokázáno.
Offline
#3 27. 01. 2015 14:38 — Editoval geovektor (27. 01. 2015 14:39)
Re: Dokaz vlasnosti
Funkciu kosinus sme si zadefinovali pomocou tayloroveho radu, teda  a myslim ze v tomto dokaze mozem pouzit to, ze viem na akom intervale funkcia sinus je rastuca a klesajuca (bez toho by sa to asi ani nedalo) dalej pozname derivaciu funkcie
a myslim ze v tomto dokaze mozem pouzit to, ze viem na akom intervale funkcia sinus je rastuca a klesajuca (bez toho by sa to asi ani nedalo) dalej pozname derivaciu funkcie  a bolzanovu vetu. To je vsetko a z toho musim vediet vyvodit dokaz no neviem ako na to.
a bolzanovu vetu. To je vsetko a z toho musim vediet vyvodit dokaz no neviem ako na to.
Offline
#4 29. 01. 2015 14:17
Re: Dokaz vlasnosti
↑ geovektor:
Ano, to je korektní definice funkce kosinus (dokonce v komplexním oboru).
Dále můžeme definovat  a derivací řady pro kosinus dostaneme řadu pro sinus a pomocí ní
a derivací řady pro kosinus dostaneme řadu pro sinus a pomocí ní
snadno zjistíme, že  (tyto úvahy jsou založeny na patřičných větách z teorie mocninných řad).
(tyto úvahy jsou založeny na patřičných větách z teorie mocninných řad).
Dosazením 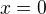 do jedné i druhé mocninné řady dostaneme
do jedné i druhé mocninné řady dostaneme
(1)  .
.
Snadno zjistíme, že  v libovolném bodě, tudíž funkce
v libovolném bodě, tudíž funkce  je konstantní.
je konstantní.
Z (1) plyne  pro libovolné
pro libovolné  .
.
Obdobným, ale poněkud složitěji provedným trikem se odvodí známé vzorce  .
.
Dále bude nutno nějak odtud zavést číslo  a zjistit průběh obou funkcí - je tedy zřejmé, že kompletní vybudování teorie
a zjistit průběh obou funkcí - je tedy zřejmé, že kompletní vybudování teorie
goniometrických funkcí uvedeným způsobem dá ještě dosti práce.
Mohu doporučit literaturu: Vojtěch Jarník: Diferenciální poet I.
Offline
#6 29. 01. 2015 15:58
Re: Dokaz vlasnosti
↑ geovektor:
Jde o to, že musíme vědět něco o čísle  . Ze vztahu
. Ze vztahu 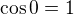 a ze spojitosti funkce cosinus plyne,
a ze spojitosti funkce cosinus plyne,
že tato funkce nabývá kladných hodnot na některém okolí nuly, odkud plyne, že množina  všech
všech
takových  , že funkce cosinus nabývá na
, že funkce cosinus nabývá na  pouze kladných hodnot , je neprázdná . Dá se
pouze kladných hodnot , je neprázdná . Dá se
též ukázat, že je shora omezená, takže má kladné a pří tom konečné supremum  , jehož dvojnásobek
, jehož dvojnásobek
značíme  .
.
Offline
#8 30. 01. 2015 10:16 — Editoval Rumburak (30. 01. 2015 13:16)
Re: Dokaz vlasnosti
↑ geovektor:
Ve zmiňované Jarníkově knize je základním vlastnostem goniometrických funkcí věnováno
několik stránek.
Jeden krok:
Dosazení 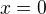 do výše uvedené mocninné řady pro
do výše uvedené mocninné řady pro 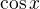 triviálně dává
triviálně dává 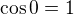 .
.
Když do téže řady dosadíme  , pak další úpravou lze odvodit, že
, pak další úpravou lze odvodit, že  .
.
Funkce 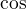 je (podle výsledků teorie mocninných řad) navíc spojitá na intervalu
je (podle výsledků teorie mocninných řad) navíc spojitá na intervalu  .
.
Podle Bolzanovy věty tak existuje  takové, že
takové, že  . Množina
. Množina  všech
všech
takových  je tedy neprázdná. Na základě spojitosti fce cosinus můžeme o ni dále říci,
je tedy neprázdná. Na základě spojitosti fce cosinus můžeme o ni dále říci,
že je uzavřená a zřejmě též omezená. Číselná množina  s těmito vlastnostmi je kompaktní
s těmito vlastnostmi je kompaktní
a má svůj nejmenší prvek - označme ho  a položme
a položme  .
.
Další krok:
Co můžeme říci o chování funkce sinus na intervalu  , víme-li dále, že
, víme-li dále, že  (viz některý můj starší příspěvek) ?
(viz některý můj starší příspěvek) ?
Offline
#9 30. 01. 2015 14:10 — Editoval geovektor (30. 01. 2015 14:30)
Re: Dokaz vlasnosti
teraz rozmyslam kam tymito uvahami smerujeme, myslim ze zo vztahu  vieme odvodit:
vieme odvodit: ![kopírovat do textarea $sin(x)= |\sqrt[2]{1-cos^2(x)}|$](/mathtex/95/95c47192e01ea52176d97faf4ca4010e.gif) mate na mysli toto? Zo vztahu
mate na mysli toto? Zo vztahu  ma nenapada nic. Tam by sa mohol nejakym sposobom upravit ten interval
ma nenapada nic. Tam by sa mohol nejakym sposobom upravit ten interval  ? Pomoze nam to nejakym sposobom? Knihu Vojtěch Jarník: Diferenciální poet I. som pozeral v Martine v kniznici, maju ju tam, takze si ju pozicam ked tam pojdem, najblizsie asi ohladom bakalarky. Diki.
? Pomoze nam to nejakym sposobom? Knihu Vojtěch Jarník: Diferenciální poet I. som pozeral v Martine v kniznici, maju ju tam, takze si ju pozicam ked tam pojdem, najblizsie asi ohladom bakalarky. Diki.
Offline
#10 30. 01. 2015 14:57
Re: Dokaz vlasnosti
↑ geovektor:
Z již dokázaného (nebo aspoň vyjasněného) jsem se chtěl dostat k tomu, že funkce sinus je na intervalu 
rostoucí a zobrazuje ho na  . Tím máme základní představu o průběhu obou funkcí na uvedeném intervalu.
. Tím máme základní představu o průběhu obou funkcí na uvedeném intervalu.
Dále: z řad pro cosinus a sinus triviálně plynou vztahy 
Budeme ještě potřebovat vzorce
 .
.
Dokazují se tak, že se vezme funkce
![kopírovat do textarea $F(x, y) := [\sin(x + y) - (\sin x \cos y + \cos x \sin y)]^2 + [\cos(x + y) - (\cos x \cos y - \sin x \sin y)]^2$](/mathtex/9b/9b6d1ad24a3092f30b53e3d629c156c3.gif)
a jejím zderivováním podle  resp. podle
resp. podle  se ukáže, že je konstantní. Dosazení
se ukáže, že je konstantní. Dosazení 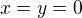 dá
dá  ,
,
odtud ony vzorce. Z nich dosazováním čísla  a jeho celočíselných násobků za proměnnou
a jeho celočíselných násobků za proměnnou  dostáváme další vztahy
dostáváme další vztahy
a vlastně všechno, co potřebujeme o průběhu těchto funkcí vědět.
Offline
#12 30. 01. 2015 15:45 — Editoval Rumburak (30. 01. 2015 15:46)
Re: Dokaz vlasnosti
↑ geovektor:
To  je nejmenší prvek množiny
je nejmenší prvek množiny  , jejíž neprázdnost plyne z B. věty, jak podrobně vysvětleno v ↑ Rumburak: .
, jejíž neprázdnost plyne z B. věty, jak podrobně vysvětleno v ↑ Rumburak: .
Offline
#14 09. 02. 2015 10:11 — Editoval Rumburak (10. 02. 2015 16:22)
Re: Dokaz vlasnosti
↑ geovektor:
Minulý týden jsem byl mimo web (proto jsem v ↑ Rumburak: nastínil celkový plán), takže můžeme pokračovat,
je-li to ještě aktuální. Podotýkám, že jsem nic nedokázal, jen jsem k tomu podal návod, jednotlivé kroky nutno
provést podrobně. Který z nich není ještě jasný ?
Poznámka:
Na tom intervale
predsa cosinus nadobuda zapornu hodnotu, takze plati bolzanova veta.
Bolzanova věta platí nezávisle na tom, zda cosinus nabývá na  záporných hodnot, či ne. Ale když nabývá,
záporných hodnot, či ne. Ale když nabývá,
pak lze B. větu použít díky tomu, že jde o spojitou funkci nabývající v 0 kladné hodnoty - viz předpoklady B. věty.
Taková je logika věci.
Offline
#15 12. 02. 2015 19:42
Re: Dokaz vlasnosti
Ano je to aktualne, za ten tyzden som rozmyslal ako to riesit a bol som aj za jednym matikarom, on mi povedal ze ku dokazaniu tychto vlastnosti nie je potrebna bolzanova veta a povedal ze to nevie dokazat s bolzanovou vetou takze som moc nepostupil a ja sam to akosi celkovo nechapem ten Vas postup, neviem no.
Offline
#16 12. 02. 2015 20:55 — Editoval jarrro (12. 02. 2015 20:56)
Re: Dokaz vlasnosti
nemá sa urobiť len klasický priebeh funkcie kosínus teda skúmať kde je derivácia kladná a kde záporná ?
Bolzanova veta je tam spomenutá preto, lebo zaručuje , že stačí rozdeliť definičný obor nulovými bodmi derivácie na intervaly a na tých intervaloch potom derivácia (-sin, ktorá je spojitá) nemení znamienko teda kosínus tam nemení monotónnosť
MATH IS THE BEST!!!
Offline
#19 13. 02. 2015 11:33 — Editoval Rumburak (13. 02. 2015 13:28)
Re: Dokaz vlasnosti
↑ geovektor:
Zkusím to dát do trochu širšího kontextu.
Chceme-li dokázat, že funkce kosinus definovaná součtem příslušné řady je např. klasající na intervalu 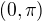 ,
,
pak musíme rovněžtak vědět, co je číslo  . Mohli bychom vyjít z klasických geometrických představ a definovat
. Mohli bychom vyjít z klasických geometrických představ a definovat jako polovinu délky kružnice o poloměru 1. Odvození vztahů takto definovaného čísla
jako polovinu délky kružnice o poloměru 1. Odvození vztahů takto definovaného čísla  k funkci kosinus
k funkci kosinus
definované řadou je sise možné, avšak poněkud krkolomné. Matematická analýza nabízí jinou cestu: číslo 
odvodit rovnou z předpisu pro funkci kosinus (tedy z řady), a sice pomocí Bolzanovy věty, jak naznačeno v mém
příspěvku z 30.1.
Jde tedy o poněkud jiný přístup, než jaký známe ze SŠ, kde se číslo  i gon. fce se odvozují z kružnice. Pomocí
i gon. fce se odvozují z kružnice. Pomocí
prostředků matematické analýzy lze zavést a studovat gon. fce a číslo  nezávisle na geometrii a geometrické
nezávisle na geometrii a geometrické
souvislosti pak prokázat dodatečně.
Matematický důkaz se ovbykle skládá z konečné posloupnosti dílčích kroků, z nicž každý je nutno pochopit,
máme-li rozumět celku. Co KONKRETNĚ není jasné v postupu, který jsem navrhl ?
Offline
#20 13. 02. 2015 23:06 — Editoval geovektor (13. 02. 2015 23:22)
Re: Dokaz vlasnosti
ok, celu nasu diskusiu som si precital este raz a myslim ze nerozumiem nasledovnym bodom:
Hned vo vasom prvom prispevku ste uviedli:  , tomuto trochu nerozumiem, nema to byt nahodou rovne jednicke?
, tomuto trochu nerozumiem, nema to byt nahodou rovne jednicke?
Dalej nerozumiem vo vasom stvrtom prispevku jednej vete, dovolim si vas citovat: pak další úpravou lze odvodit, že  . Tomuto trosku nerozumiem ako to tak snadno je mozne ukazat.
. Tomuto trosku nerozumiem ako to tak snadno je mozne ukazat.
A tiez by som sa chcel spytat ze vo vasom druhom prispevku ste napisali, opat citujem: Dále můžeme definovat  Toto sme odvodili zo vztahu
Toto sme odvodili zo vztahu  ???
???
Offline
#21 14. 02. 2015 11:25 — Editoval jarrro (14. 02. 2015 11:27)
Re: Dokaz vlasnosti
geovektor napsal(a):
Hned vo vasom prvom prispevku ste uviedli:
, tomuto trochu nerozumiem, nema to byt nahodou rovne jednicke?
Všimni si ten znak derivácie
geovektor napsal(a):
Dalej nerozumiem vo vasom stvrtom prispevku jednej vete, dovolim si vas citovat: pak další úpravou lze odvodit, že
. Tomuto trosku nerozumiem ako to tak snadno je mozne ukazat.
dosdením do radu pre kosínus
A tiez by som sa chcel spytat ze vo vasom druhom prispevku ste napisali, opat citujem: Dále můžeme definovat
Toto sme odvodili zo vztahu
???
mysím, že Rumburak predpokladá, že nič okrem rozvoja kosínusu do taylorovho radu sa nepozná
Podľa mňa mal zadávateľ na mysli obyčajný priebeh funkcie s tým, že priebeh sínusu a vlastnosti čísla pi sú už známe
spýtaj sa zadávateľa či preibeh sínusu možno považovať za známy ak áno tak je to klasický prebeh funkcie teda nájdenie nulových bodov derivácie a kukanie kde derivácia je kladná a kde je záporná
MATH IS THE BEST!!!
Offline
#22 14. 02. 2015 23:36 — Editoval geovektor1 (14. 02. 2015 23:41)
- geovektor1
- Příspěvky: 119
- Reputace: 0
Re: Dokaz vlasnosti
Jarrro dakujem Vam za vase tri odpovede, pomohli ste mi pochopit vsetky tri otazky. Takze teraz sa pokusim zosumarizovat co vieme a idem nacrtnut moj prvy naznak dokazu, snad to nejako spolocne zvladneme.
Takze:
Ak to spravne chapem, tak vlastnosti ktore nebudeme dokazovat, ktore "vieme" su:
1, Sinus nadobuda kladne hodnoty na 
2, Sinus nadobuda zaporne hodnoty na 
3, Funkcia sinus je spojita
Z tohoto bezprostredne vypliva, ze hodnoty v krajnych bodoch su nulove. To je poznatok, ktory sme odvodili z predchadzajucich troch
Z podmienky 1, a derivacie vieme ze  je
je 
Z podmienky 2, a derivacie vieme ze  je
je 
Dalej vieme, ze:  a
a 
Vieme ze  a z toho odvodime:
a z toho odvodime: 
Dalej vieme ze  a tiez vieme ze cosinus je spojita funkcia takze musi existovat take
a tiez vieme ze cosinus je spojita funkcia takze musi existovat take  ze funckia cosinus nadobuda na intervale
ze funckia cosinus nadobuda na intervale  a myslim ze aj na
a myslim ze aj na  kladne hodnoty.
kladne hodnoty.
Dalej polozime  , to mozeme pretoze
, to mozeme pretoze  a
a  a plati bolzanova veta, takze musi existovat
a plati bolzanova veta, takze musi existovat  take ze
take ze  a
a 
Dalej pozname vztahy: 
a 
a
![kopírovat do textarea $F(x, y) := [\sin(x + y) - (\sin x \cos y + \cos x \sin y)]^2 + [\cos(x + y) - (\cos x \cos y - \sin x \sin y)]^2$](/mathtex/9b/9b6d1ad24a3092f30b53e3d629c156c3.gif)
Tu by som asi nejako takto zastal, priznam sa ze poslednemu vztahu nerozumiem, metie ma toto:  co znamena ten vztah toho eFka s tymi x,y premennymi?
co znamena ten vztah toho eFka s tymi x,y premennymi?
Offline
#23 17. 02. 2015 11:33 — Editoval Rumburak (17. 02. 2015 11:38)
Re: Dokaz vlasnosti
↑ geovektor1:
Shrnul bych to asi takto:
I. Základními vztahy jsou :
(1)  ,
,
(2)  ,
,
(3)  ,
,
(4)  .
.
Jako definice lze vnímat buďto vztahy (1), (2) (že obě řady v uvedeném rozsahu konvergují, by se muselo zdůvodnit)
a z nich odvodit (3), (4),
nebo vzít jako definice vztahy (1), (3) a z nich odvodit (2), (4) ,
případně vzít jako definice vztahy (2), (4) a z nich odvodit (1), (3).
Všechny tyto přístupy jsou ekvivalentní.
Odtud se odvozováním či dokazováním obdrží:
II. Funkce  jsou v libovolném
jsou v libovolném 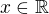 spojité a mají konečné derivace všech řádů.
spojité a mají konečné derivace všech řádů.
III. Pro libovolné 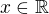 je
je
(5)  .
.
IV. Dosazením  do (1), (2) dostáváme
do (1), (2) dostáváme
(6)  .
.
V. Z (3), (4) plyne (podle vět o aritmetice derivací a o derivaci složené funkce)  ,
,
takže funkce  je konstantní , odtud a podle (6) pak
je konstantní , odtud a podle (6) pak
(7)  .
.
VI. Úpravou vzorce (2) dostáváme  ,
,
speciálně pro  je
je .
.
Snadno nahlédneme, že všechny uzávorkované výrazy v poslední nekonečné řadě představují kladná čísla, odtud .
.
O funkci 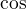 tedy máme zjištěno, že je spojitá na intervalu
tedy máme zjištěno, že je spojitá na intervalu  , při čemž
, při čemž  .
.
Podle Bolzanovy věty tedy existuje  takové, že
takové, že  . Kolik takových
. Kolik takových  existuje, to B. věta naříká.
existuje, to B. věta naříká.
Avšak na základě spojitosti funkce 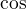 lze dokázat, že mezi nimi existuje jedno takové, které je znich nejmenší.
lze dokázat, že mezi nimi existuje jedno takové, které je znich nejmenší.
Toto číslo označme  .
.
VII. Takže na intervalu  nabývá funkce
nabývá funkce 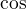 pouze kladných hodnot. Tedy funkce
pouze kladných hodnot. Tedy funkce 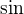 má na tomto intervalu
má na tomto intervalu
kladnou derivaci (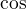 ), proto je zde rostoucí a vzhledem ke spojitosti v nule (a hodnotě
), proto je zde rostoucí a vzhledem ke spojitosti v nule (a hodnotě  ) kladná.
) kladná.
Na uvedeném intervalu je 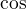 naopak klesající (má zde zápornou derivac
naopak klesající (má zde zápornou derivac  ).
).
Pomocí vztahů (5) lze pak snadno rozhodnout o průběhu obou funkcí na intervalu  . Pomocí spojitosti obou
. Pomocí spojitosti obou
funkcí můžeme učinit závěry o jejich průběhu na intervalu  - na základě druhých derivací i pokud jde
- na základě druhých derivací i pokud jde
o konvexnost resp. konkávnost.
Zbytek doplním později.
Offline
#24 17. 02. 2015 19:45
- geovektor1
- Příspěvky: 119
- Reputace: 0
Re: Dokaz vlasnosti
tomuto zatial rozumiem, a aky zbytok chcete doplnit neskor? Toto nie je cely dokaz?
Offline
#25 18. 02. 2015 09:57 — Editoval Rumburak (18. 02. 2015 14:09)
Re: Dokaz vlasnosti
↑ geovektor1:
Zatím máme (alespoň v pricnipu) vyšetřen průběh funkcí  pouze na inervalu
pouze na inervalu  .
.
K dalšímu budeme potřebovat vzorce pro součet argumentů, které ještě odvozeny nemáme. K tomu položme
 ,
,
kde 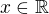 je funkční proměnná, zatímco
je funkční proměnná, zatímco  prozatím vnímáme jako libovolnou, avšak pevně zvolenou
prozatím vnímáme jako libovolnou, avšak pevně zvolenou
konstantu (abychom se vyhnuli teorii funkcí více proměnných). Snadno zjistíme, že  .
.
Odtud obdobně jako v IV. odvodíme, že  , takže
, takže  je konstantní
je konstantní
funkce. Zřejmě  , takže
, takže  a odtud
a odtud  .
.
Tím jsou vzorce

dokázány. Dosazením  máme
máme

(že  plyne z předchozích výsledků) a odtud můžeme získat poznatky o průběhu funkcí
plyne z předchozích výsledků) a odtud můžeme získat poznatky o průběhu funkcí 
na intervalu  atd.
atd.
Mimo to klademe  .
.
Offline
