Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Důkaz vztahu derivace a monotonie
#1 30. 03. 2017 12:00
Důkaz vztahu derivace a monotonie
Dobrý den,
existuje nějaký jednoduchý způsob, jak z běžných vět elementární analýzy dokázat, že má-li funkce na intervalu nezáporné jednostranné derivace, je na něm neklesající? Důkaz, který mám, nevyžaduje nic než definici jednostranných derivací, ale je pro cílovou skupinu, tj. studenty, dosti komplikovaný. Předem děkuji.
Offline
#3 30. 03. 2017 13:03 — Editoval Cynyc (30. 03. 2017 13:32)
Re: Důkaz vztahu derivace a monotonie
↑ Bati: Ani jedno, spíše mě nenapadlo, že "nezáporné jednostranné derivace" bude někdo interpretovat jako "jednu nezápornou jednostrannou derivaci". Takže pro jistotu: má-li funkce na intervalu nezáporné OBĚ jednostranné derivace, je na něm neklesající.
Offline
#4 01. 04. 2017 13:58
Re: Důkaz vztahu derivace a monotonie
↑ Cynyc:
Ok. Jako učitel bys to ale měl formulovat precizně. Neříkám, že to je nutně tvůj případ, ale na střední mě nejvíc vytáčeli vyučující, kteří dali nejednoznačný zadání příkladů a navíc očekávali že vždycky dostanou přesně to řešení, který měli někde na papíře předem napsaný.
K tvojí otázce: V podstatě se stačí podívat do důkazu věty o střední hodnotě a malinko ho poupravit. Proč? Pokud by daná funkce měla klasickou nezápornou derivaci, pak podle obyčejné věty o stř. hodnotě dostaneš  pro lib.
pro lib.  , odkud plyne monotonie. Ve skutečnosti by ti tady ale stačilo vědět, že existuje nějaké c, pro které
, odkud plyne monotonie. Ve skutečnosti by ti tady ale stačilo vědět, že existuje nějaké c, pro které  leží mezi body
leží mezi body  a
a  , protože oba jsou
, protože oba jsou  . Proč by takové c mělo existovat pro funkci, která má pouze jednostranné derivace je intuitivně vidět z grafu např. absolutní hodnoty. Abys to dokázal, stačí fakt jen zopakovat důkaz VoSH pomocí základního tvrzení, že spojitá funkce na uz. intervalu nabývá minima a maxima (spojitost samozřejmě máš).
. Proč by takové c mělo existovat pro funkci, která má pouze jednostranné derivace je intuitivně vidět z grafu např. absolutní hodnoty. Abys to dokázal, stačí fakt jen zopakovat důkaz VoSH pomocí základního tvrzení, že spojitá funkce na uz. intervalu nabývá minima a maxima (spojitost samozřejmě máš).
Offline
#5 01. 04. 2017 19:04 — Editoval Cynyc (01. 04. 2017 20:13)
Re: Důkaz vztahu derivace a monotonie
↑ Bati: Jednostranné rozšíření Rolleovy resp. Lagrangeovy věty je triviální, to normálně vykládám. Problém není v jednostrannosti, ale v absenci předpokladu spojitosti, kterou "samozřejmě" nemám. Takže i kdybych uznal, že formulace o derivacích byla nejednoznačná, stejně interpretujete moje zadání chybně i v tom, co jednoznačné je.
Oprava: jak se ukazuje níže, nejde o chybnou intepretaci, ale důsledek užití jiné, neekvivalentní definice.
Offline
#9 01. 04. 2017 19:55 — Editoval Cynyc (01. 04. 2017 20:14)
Re: Důkaz vztahu derivace a monotonie
↑ Bati: Nerozumím. -sgn má v nule zápornou derivaci, takže pokud v inkriminovaném intervalu bude (alespoň jednostranně) nula, není splněn předpoklad nezápornosti derivace, a pokud ne, je na daném intervalu neklesající.
Co se týče nevlastních derivací, považoval jsem je za standard; literatura, z níž čerpám (Jarník, Veselý aj.) shodně nevlastní derivace připouští, proto mě nenapadlo to zdůrazňovat. Teď ale koukám, že třeba definice derivace na anglické wikipedii, ač formálně stejná, zjevně nevysloveně připouští jen konečné derivace. Jde tedy, jak jsem uvedl již výše, o nedorozumění vyplývající z odlišných definic. Pokud připustíme jen vlastní derivace, pak skutečně již máme při jejich existenci spojitost, příslušné věty ovšem potom neplatí ani pro řadu běžných elementárních funkcí jako ![kopírovat do textarea $\sqrt[3]{x}$](/mathtex/53/537f3e3eae88063acab693151571f957.gif) .
.
Offline
#10 01. 04. 2017 19:58 Příspěvek uživatele Bati byl skryt uživatelem Bati. Důvod: uz vysvetleno
#13 01. 04. 2017 20:22 — Editoval Bati (01. 04. 2017 20:24)
Re: Důkaz vztahu derivace a monotonie
↑ Cynyc:
Tak co se týče spojitých funkcí s nevlastními derivacemi, tam ta úprava důkazu věty o střední hodnoty projde stejně, ne? Tím pádem zbývá vyřešit skoky. Ty můžou být zjevně jen neklesající a když je odečtu, tak dostanu spojitou funkci s nezměněnou derivací vyjma těch skoků.
Offline
#15 01. 04. 2017 21:36
Re: Důkaz vztahu derivace a monotonie
↑ Cynyc:
No, prostě bych odečetl po částech konstantní funkci, která by odpovídala těm skokům, to je přece jedno, kolik by jich tam bylo. Spojitost mi nepřijde jako problém, spíš teď nevidím, jak obejít to, že v těch "zespojitěných" bodech neznám jednostranné derivace.
Offline
#16 01. 04. 2017 23:13 — Editoval Cynyc (02. 04. 2017 10:18)
Re: Důkaz vztahu derivace a monotonie
↑ Bati: K definici té po částech konstantní funkce je podle mě nutný součet přes obecnou podmnožinu R, což je konstrukce, která studentům v době, kdy se řeší vztah derivace a monotonie, zdaleka není známa (a na naší škole se s ní neseznamují ani později, jen s obyčejnými řadami). Co se týče derivací v zespojitěných bodech, ty nemusejí existovat - vezměte si libovolnou spojitou neklesající funkci, která v nějakém bodě nemá derivaci třeba zprava, a posuňte funkční hodnotu v tomto bodě dolů. Pak bude mít díky skoku zprava nekonečnou derivaci.
Offline
Stránky: 1
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Důkaz vztahu derivace a monotonie

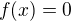 na
na ![kopírovat do textarea $(0,1]$](/mathtex/49/49a91ace7e5edc0bde75d00d14360088.gif) ,
,  na
na 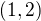 má nezápornou derivaci zleva všude v
má nezápornou derivaci zleva všude v  a přesto tam není neklesající. Z toho mi vychází, že jsi buď neuvedl nějaké předpoklady, anebo tvůj důkaz je špatně.
a přesto tam není neklesající. Z toho mi vychází, že jsi buď neuvedl nějaké předpoklady, anebo tvůj důkaz je špatně. a existence takové derivace spojitost nijak nezaručuje. Příkladem je funkce signum v nule.
a existence takové derivace spojitost nijak nezaručuje. Příkladem je funkce signum v nule. pro
pro  . Jedině, že bys uvažoval nekonečný derivace, ale to by bylo vhodný předem zmínit.
. Jedině, že bys uvažoval nekonečný derivace, ale to by bylo vhodný předem zmínit.