Matematické Fórum

Ahoj,
následující není úloha, ale spíše úvaha. Děkuji předem za polemiku s ní.

Nechť je dána úplná teorie T (tj. každá uzavřená formule nebo její negace je dokazatelná) s predikátem rovnosti.
Označme jako S(n) tvrzení "existuje n různých prvků". Formálně lze např. S(3) vyjádřit jako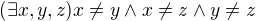
(a pro každé n lze výrok S(n) podobně formálně zapsat).
Potom pokud by existovaly pro m<n modely M(m) a M(n) teorie T o počtu prvků m a n, tak by v M(m) nemohlo platit S(n), které platí v M(n) - a tedy by S(n) ani jeho negace neplatilo současně v obou modelech M(m) a M(n) a tedy by S(n) ani jeho negace nemohla být dokazatelná, což je spor s úplností T. Tedy pokud má T nějaké konečné modely, tak musí mít všechny stejnou mohutnost.

A pokud bychom dovedli nějak formalizovat výroky P(K) tvaru "Existuje množina stejné mohutnosti jako kardinál K" (pro libovolný kardinál K), tak bychom stejnou úvahou mohli dospět k tomu, že všechny modely teorie T musí mít stejnou mohutnost. Případně, že všechny modely o menší mohutnosti než jistý kardinál L (pokud bychom dovedli P(K) formalizovat jen pro K o menší mohutnosti než L) mají stejnou mohutnost.

Je ve výše uvedených úvahách nějaká chyba? Pokud ne, tak je to docela zajímavé zjištění.