Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 05. 2009 15:02
Goniometrické rovnice
Zdravím všechny matematiky. mám tu příklad na goniometrické rovnice a nevím proč je počet řešení ve výsledku 3.
rovnice zní.
odmocnina ze 2 (sin^2x - cos^2x) = -1
v intervalu <0,3/2pi>
prosím taky o kontrolní výpočet nevím jestli můj postup je správný. Já si myslím,že řešení jsou dvě nevím kde mám chybu.
Offline
#3 18. 05. 2009 20:00
- marnes

- Příspěvky: 11227
Re: Goniometrické rovnice
↑ lenisek:
odmocnina ze 2 (sin^2x - cos^2x) = -1 závorka je - cos 2x
odm2 . cos 2x =1 dělím odmocninou a hned usměrním
cos 2x=odm2/2 sub
cos u=odm2/2
u´= 45 st
u1=135 st + k.360 st
u2=225 st + k.360 st
x1=67,5st + k.180 st
x2=112,5 st + k.180 st
řešení x1=67,5
x2=135
x3=202,5
x4=270
x5=112,5
x6=225
Tak teď nevím, mě jich vyšlo celkem 6. Leda bych ještě špatně pochopil tůj zápis. Ale návod by tam měl být
Jo. A na začátku vás zdravím.
Offline
#6 19. 05. 2009 07:17
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Goniometrické rovnice
↑ lenisek:
Tak jak jsem to pochopil já, tak mě vychází v předmětném intervalu 2 řešení:
Nikdo není dokonalý
Offline
#9 19. 05. 2009 08:55 — Editoval jelena (19. 05. 2009 08:58)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Goniometrické rovnice
Zdravím vás,
marnes napsal(a):
u´= 45 st
u1=135 st + k.360 st
u2=225 st + k.360 st
myslím, že tady bude malý překlep:
pokud  , pak u_1 = 45, u_2 = 315 (periody, dopočty pro x atd.)
, pak u_1 = 45, u_2 = 315 (periody, dopočty pro x atd.)
Může být?
-------------
Odpusť, Oline!
Offline
#12 19. 05. 2009 09:38
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Goniometrické rovnice
můžete mi někdo napsat jak se počítá toto?
řešte rovnici  pro
pro 
Offline
#14 19. 05. 2009 09:45 — Editoval marnes (19. 05. 2009 09:46)
#15 19. 05. 2009 10:04
#16 19. 05. 2009 10:15
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Goniometrické rovnice
↑ Cheop: takto jsem to taky počítal, ale nechápu když máš 2cos^2x=1/2 jak jsi dostal cosx=+-1/2??
Offline
#17 19. 05. 2009 10:29 — Editoval Cheop (19. 05. 2009 10:30)
#19 19. 05. 2009 10:45
- vonSternberk
- Příspěvky: 269
- Reputace: 0
Re: Goniometrické rovnice
chci se ještě zeptat na toto:
řešte rovnici  pro
pro 
já se zasekkl hned na začátku, jen toto jsem vymyslel:
Offline
#20 19. 05. 2009 10:48
Re: Goniometrické rovnice
↑ vonSternberk:
goniometricka jednicka s uhlem x/2: 
dvojnasobny uhel v argumentu cosinu: 
a mas vsechno s argumentem  .
.
Offline
#22 19. 05. 2009 11:56
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Goniometrické rovnice
↑ vonSternberk:
1)  substituce
substituce 
 vratka k substituci:
vratka k substituci:
2) 
Řešení:
Nikdo není dokonalý
Offline

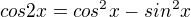
 což jsou opravdu 3 požadovaná řešení.
což jsou opravdu 3 požadovaná řešení.



 , takže tam moje x_3 patří, ale celej příklad stejně padá na prvním řádku :-)
, takže tam moje x_3 patří, ale celej příklad stejně padá na prvním řádku :-)