Matematické Fórum

Roscelinius · 05. 12. 2019 08:25

Dobrý den,
prosím o pomoc s úlohou na transformaci integrálu

$\int_{0}^{c}dx\int_{\alpha x}^{\beta x} f(x,y)dy$
kde, $0<\alpha <\beta; c>0$ , do nových proměnných $u=x+y, uv=y$ .
Díky

vlado_bb

↑ Roscelinius: Aky Jacobian ti vysiel? A mimochodom, presuvam do spravnej sekcie.

Roscelinius · 05. 12. 2019 13:21

↑ vlado_bb:

Jakobián mi vyšel (x+y). Nevím jestli můžu a jak použít větu o transformaci integrálu, když vlastně nejde o jeden dvojný integrál ale o součin dvou různých integrálů. Díky za objasnění.

Rumburak · 05. 12. 2019 13:32

↑ Roscelinius:

Ahoj.

Při integraci podle n integračních proměnných existuje rozdíl mezi integrálem n-násobným a n-rozměrným.
Standardní věta o substuci je uváděna ve tvaru pro integrál n-rozměrný, tedy v případě n= 2 pro integrál
dvojrozměrný neboli dvojný. Toto

(1) $\int_{0}^{c}dx\int_{\alpha x}^{\beta x} f(x,y)dy$

ovšem není integrál dvojný, ale dvojnásobný. Prvním krokem k vyřešení úloby by proto mělo být
vyjádření inegrálu (1) ve tvaru integrálu dvojného.

Rumburak

↑ Roscelinius:
PS. Zdá se, žes na důležitou věc kápnul sám. Avšak o součin integrálů by šlo, pokud by druhý integrál nezávisel
na proměnné x, což ale splněno není . O něco přesnější zápis by měl tvar

$I = \int_{0}^{c}\int_{\alpha x}^{\beta x} f(x,y)dydx$ .

Zkus určit množinu M v R2 tak, aby

$I = \iint_M f(x,y) dydx$ .

Roscelinius

Co toto mé řešení?
$\varphi: (x,y) \rightarrow (u,v)=(x+y, \frac {y}{x+y})$
jakobián: $|det D\varphi ^{-1}|=x+y=u=> |det D\varphi|=\frac{1}{u}$
nové meze:
y $y_{0} \rightarrow v_{0}: u=x+y_{0}, uv_{0}=x+y_{0}:=>v_{1}= \frac{\alpha }{1+\alpha},v_{2}= \frac{\beta }{1+\beta}$
$x_{0} \rightarrow u_{0}: u_{0}=x_{0}+y , u_{0}v=y=>u_{1}= 0, u_{2}=\frac{c}{1-v}$
pak:
$\int_{0}^{c}dx \int_{\alpha x}^{\beta x} f(x,y) dy= \int_{0}^{c} \int_{\alpha x}^{\beta x} f(x,y) dydx= \int_{0}^{\frac{c}{1-v}} \int_{\frac{\alpha }{1+\alpha}}^{\frac{\beta }{1+\beta}} (f(x,y)\circ \varphi)\frac{1}{u} dv du=$
$=\int_{\frac{\alpha }{1+\alpha}}^{\frac{\beta }{1+\beta}} \int_{0}^{\frac{c}{1-v}} (f(x,y)\circ \varphi)\frac{1}{u} \ du dv$
Dělám někde chybu? Nevím jestli ten Jakobián je skurtečně od inverzního zobrazení, mám v tom už zmatek.
Díky

krakonoš

↑ Roscelinius:
Myslim, že jakobian by měl být u, protože jsme vyjádřili souřadnice jako
stara souřadnice=kombinace nových ,tj x=u-uv;y=uv,*
Podobně je to i u substituce u jednoduchých integrálů, stačí si uvědomit příklady na první a druhou substiuci.
Pokud si pamatuji správně, myslím ale že je ve větě absolutní hodnota jakobiánu.Navíc má být zobrazení x,y >u,v proste, myslím, na internetu jsem znění věty nenašla.,ale mělo by to odpovídat druhé substituční metodě v případě vyjádření*, tam je taky abs hodnota.
Jedině mi je divné, že v učebnici , kterou mám(Kalenda, Metody reseni....) neni u druhe substitucni metody požadavek na nenulovou derivaci, zatimco u transformace u dvojnych integralu se prece pozaduje regularita zobrazeni, kdy ma byt jakobian nenulovy.Chtelo by to znat presne zneni vet.

Roscelinius · 05. 12. 2019 21:35

↑ krakonoš: To sice ano ale první jakobián je z jakobiho matice která derivuje u,v podle x,y, což je opačně než by mělo být, protože se má derivovat staré souřadnice podle nových. Použil jsem inverzní jakobián protože se derivace počítají snadněji. Meze mám spočítané správně?

krakonoš

↑ Roscelinius:
Řekla bych, že záleží na funkci, kterou integrujeme.
U jednoduchých integrálů typu
$\int_{}^{}e^{-2x}dx$ volíme 1. substituční metodu a substituci y=-2x,
zatímco u integrálů typu
$\int_{}^{}\frac{1}{\sqrt{1-x^{2}}}dx$ je vhodná sibstituční metoda 2.
x=sin y.
Máme-li $\int_{}^{}\int_{}^{}e^{-x^{2}-y^{2}}dxdy$ bude vyhovovat druhá substituční x= ...y=...., takže bych řekla, že tady nejde o to jaké derivace se ti počítají snadněji, ale půjde o konkrétní vyjádření f(x,y)
Pokud se ti hodí 1. subs metoda, bude jakobián, jak píšeš.
U těch mezí se mi nezdá, když x začlo běžet od nuly, y začlo od alfa *x, tak v=y/x+y by mělo být od jedné......Ty meze máš divné, sám vidíš, když ve vnitřním integrálu integruješ podle v a dosadíš konstanty, nemůže v horní mezi vnějšího integrálu figurovat v........
Možná to brát, že u je součet, tak by mělo proběhnout od nuly do c+beta c, v brát jako 1-(x/(u)), kde x proběhlo od nuly do c...

Roscelinius · 06. 12. 2019 07:38

krakonoš napsal(a):
↑ Roscelinius:
.., když x začlo běžet od nuly, y začlo od alfa *x, tak v=y/x+y by mělo být od jedné......

podle mého meze určuješ vždy z jedné staré proměnné, druhou pokud v zobrazení figuruje si vyjádříš v nových proměnných.
U posledního výrazu když integruji vnitřní integrál podle u, je sice v horní mezi v ale to se mi odintegruje v další integraci podle v. Proto jsem integrály prohodil aby dávali lepší geometrický smysl.

Bati · 06. 12. 2019 22:41

Tu inverzi uz mas skoro explicitne v zadani:
$F(u,v)=(u(1-v),uv)$ . Chces najit meze pro $u,v$ , aby $F(u,v)=(x,y)$ prave kdyz $x,y\in T$ , kde $T$ je puvodni mnozina v integralu (trojuhelnik). Jsi vlastne v podobne situaci jako napr. pri transformaci do polarnich souradnic. Ze vsech nerovnosti ti musi vyjit
$0<u<c(\beta+1)$ ,
$\max(1-\frac cu,\frac{\alpha}{\alpha+1})<v<\min(1,\frac{\beta}{\beta+1}))=\frac{\beta}{\beta+1}$
Protoze $|DF|=u$ , tak vyjde
$\int_{0}^{c}dx\int_{\alpha x}^{\beta x} f(x,y)dy=\int_0^{c(\beta+1)}\int_{\max(1-\frac cu,\frac{\alpha}{\alpha+1})}^{\frac{\beta}{\beta+1}}f(u(1-v),uv)u\,\mathrm{d}v\,\mathrm{d}u$ , coz je taky to samy jako
$\int_0^{c(\alpha+1)}\int_{\frac{\alpha}{\alpha+1}}^{\frac{\beta}{\beta+1}}f(u(1-v),uv)u\,\mathrm{d}v\,\mathrm{d}u+\int_{c(\alpha+1)}^{c(\beta+1)}\int_{1-\frac cu}^{\frac{\beta}{\beta+1}}f(u(1-v),uv)u\,\mathrm{d}v\,\mathrm{d}u$ .
Dale, pokud mas zavisly meze, nemuzes jen tak prohazovat integraly, protoze to ani nedava smysl!

Roscelinius · 08. 12. 2019 10:03

↑ Bati:
Děkuji. konečně jsem si ujasnil jak je to s tou inverzí.
Mohl bys mi prosím ještě trochu podrobněji rozepsat jak jsi získal ty nové meze z toho trojúhelníka? díky

Bati · 08. 12. 2019 11:06 — Editoval Bati (08. 12. 2019 11:07)

↑ Roscelinius:
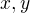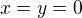Kdyz $u=x+y$ a $x,y$ jsou z mnoziny $\{0<x<c,\;\alpha x< y<\beta x\}$ , tak minimum $u$ dostanu pro $x=y=0$ a maximum $u$ pro $x=c$ , $y=\beta x=\beta c$ , tudiz $0<u<c+\beta c=c(\beta+1)$ . Pak $v$ musi byt takove, aby platilo
$0<u(1-v)<c$
$\alpha u(1-v)<uv<\beta u(1-v)$
(jenom jsem prepsal podminky pro x a y pomoci u a v). Upravou tech nerovnic dostanes meze pro v.