Matematické Fórum

Pomeranc · 26. 05. 2020 23:29

Ahoj,

nevím si rady s touto úlohou:
//forum.matweb.cz/upload3/img/2020-05/28384_PAST_MinMaxkonvergence.PNG

Problém je, že i když znám hustotu maxima i minima a rovnoměrného rozdělení, tak se mi to nedaří dát dohromady.
Další problém je, jak mám vyšetřit konvergenci Xn k něčemu, pokud znám jen hustotu rozdělení Xn.

Nevíte prosím někdo jak na to?

Stýv · 27. 05. 2020 01:35

Další problém je, jak mám vyšetřit konvergenci Xn k něčemu, pokud znám jen hustotu rozdělení Xn.

Co bys ještě chtěla znát?

Pomeranc · 27. 05. 2020 12:49

↑ Stýv:

Já neříkám, že nemám informací dost, naopak hustota nám toho říká hodně,
ale nevím, jak to mám spočítat, když tam mám zadanou hustotu.

Stýv · 27. 05. 2020 14:01

↑ Pomeranc:
1) jaké je rozdělení Y_n?
2) co znamená konvergence v distribuci?

Pomeranc · 27. 05. 2020 22:54

↑ Stýv:

1) Nechť Vn = min{X1,...,Xn}, když neznáme přesné rozdělení Xn,
tak obecně $f_{v}=n*[1-F(v)]^{n-1}*f(v)$ .
Distribuční funkci rovnoměrného rozdělení známe.
Když jsem se to snažila dát dohromady:
$f_{v}=0$ všude jinde než na [0,1]
$f_{v}=n*[1-v]^{n-1}$ na [0,1]

2) posloupnost Xn konverguje X v distribuci, jestliže posloupnost jednotlivých rozdělení Xn
konverguje k rozdělení X.
Bohužel vztahy mezi konvergencí v distribuci a skoro jistě jsme mi neříkali, a tak
nevím, jestli pokud se mi podaří dokázat konvergenci v distribuci, jestli mi to bude implikovat konvergenci skoro jistě.

Stýv · 28. 05. 2020 00:39

↑ Pomeranc:
1) A distribuční funkce, tj P(X<=x)?

2) Ježiš sorry, já chtěl napsat "v pravděpodobnosti", tu teď dokazujem.

Pomeranc · 28. 05. 2020 00:54

↑ Stýv:

1) $Fv =0$ na (-nekonečno do a)
$Fv = 1 - [1 - v]^{n}$ na [a,b]
$Fv =1$ jinde

2) Posloupnost Xn konverguje k X v pravděpodobnosti pokud
$\forall \varepsilon >0 \lim_{n\to\infty } P(|Xn-X|>\varepsilon )=0$

Stýv · 28. 05. 2020 01:03

↑ Pomeranc: No a když $Y=0$ , kolik je $P(|Y_n-Y|>\varepsilon )$ ?

Pomeranc

↑ Stýv:

Já nevím.
$P(|Y_n-Y|>\varepsilon )$ = $P(|min{X1,..,Xn}|>\varepsilon )$

Stýv · 28. 05. 2020 08:02

↑ Pomeranc: Nevidíš souvislost mezi $P(Y_n>\varepsilon )$ a definicí distribuční funkce veličiny $Y_n$ ?

Pomeranc · 28. 05. 2020 13:11

↑ Stýv:

$P(|Y_n-Y|>\varepsilon )$ = $P(|min{X1,..,Xn}|>\varepsilon )$
Je korektní odstranit absolutní hodnotu?
$1-P(min\{X1,..Xn\}\le \varepsilon )$ = 1 na (-nekonečno do 0)
= (1-v)^n na [0,1]
= 0 jinde
$\varepsilon >0$ , tak je to rovno 0, a tedy to konverguje k 0, a tedy to konverguje v pravděpodobnosti.

Stýv · 28. 05. 2020 16:44

Pomeranc napsal(a):
Je korektní odstranit absolutní hodnotu?

Může $Y_n$ být záporné?

Dál je to trochu zmatené – $1-P(min\{X1,..Xn\}\le \varepsilon )$ je funkcí $\varepsilon$ , nikoli $v$ . Z těch tří větví nás zajímá jenom jedna, ta pro malá kladná $\varepsilon$ .

Pomeranc napsal(a):
tak je to rovno 0, a tedy to konverguje k 0, a tedy to konverguje v pravděpodobnosti

Co je které "to"?

Pomeranc · 28. 05. 2020 20:43

↑ Stýv:

Máš pravdu, Yn nemůže být záporné, kvůli tomu, že Yn má rovnoměrné rozdělení na [0,1].

Pokusím se být více přesnější
$\lim_{n\to\infty }P(|Y_n-Y|>\varepsilon )$ = $\lim_{n\to\infty }P(|min\{X1,..,Xn\}|>\varepsilon )$
To je rovno s využitím doplňkového jevu a odstraněním absolutní hodnoty
$\lim_{n\to\infty }1-P(min\{X1,..Xn\}\le \varepsilon )$ = $\lim_{n\to\infty }[1 - v]^{n}$ = 0.

Stýv · 28. 05. 2020 21:07

↑ Pomeranc: To už vypadá ok. Tak teď bod b). Co bys tipla, konverguje s. j., nebo ne?

Pomeranc · 28. 05. 2020 21:16

↑ Stýv:

Řekla, že bych že ne.
Xn jsou náhodné veličiny s rovnoměrným rozdělením na [0,1] pro všechna n,
tedy není důvod, proč by to mělo dokonvergovat k náhodné veličině, která zobrazuje vše na 0.

Stýv · 29. 05. 2020 00:58

↑ Pomeranc: Samotné Xn by nikam nedokonvergovaly, ale to minimum by mohlo. ;-) Znáš nějaké věty o vztahu mezi konvergencí v P a konvergencí s. j.?

Pomeranc · 29. 05. 2020 14:34

↑ Stýv:

Ano, mohlo by :) . My jsme si říkali, že když je splněna konvergence sj, tak je splněna i konvergence v P.
Obráceně to platit nemusí.

Nakoukla jsem do výsledků, a tam bylo napsáno Canteliho věta.

Stýv · 29. 05. 2020 15:14

↑ Pomeranc: Cantelliho věta je která? Nemám u sebe žádný materiály.

Já našel nějaký tvrzení o tom, že z konvergence v P vyplývá konvergence s. j. pro nějakou podposloupnost, což by se taky dalo použít, ale jestli ti radí Cantelliho, použijme Cantelliho.

Pomeranc · 29. 05. 2020 17:17

↑ Stýv:

Canteliho věta, jak ji známe je zde: Odkaz.

Stýv · 29. 05. 2020 18:37

↑ Pomeranc: Ok. Musel jsem teda roztočit nějaký mozkový závity, který už byly lehce zarezlý, ale myslím, že to mám. :-)

Chceš prostě poradit, jak zvolit ty jevy 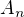$A_n$ , a pak si to dopočítáš, nebo chceš provést myšlenkovám procesem, kterým jsem si prošel já? Bude to trochu zdlouhavější, ale snad i poučnější.

Pomeranc · 29. 05. 2020 18:48

↑ Stýv:

Můžeme vyzkoušet druhou variantu a přinejhorším to změnit na první :)

Stýv · 29. 05. 2020 18:55

↑ Pomeranc: Dobře, tak začni tím, že si rozepíšeš, co v našem případě znamená ta konvergence s. j. Limitu rovnou rozepiš pomocí definice limity.

Pomeranc · 29. 05. 2020 20:01

↑ Stýv:

$P(\lim_{n\to\infty }Yn=Y)$ = $P(\forall \varepsilon >0 \exists n_{o}\forall n\ge n_{o}:|Yn-Y|<\varepsilon )$
= $P(\bigcap_{\varepsilon>0 }^{}\bigcup_{n_{0}=1}^{\infty }\bigcap_{n=n_{0}}^{\infty }Yn<\varepsilon )$
= $\prod_{\varepsilon >0}^{}P(\liminf_{n\to\infty } Yn<\varepsilon )$ = $\prod_{\varepsilon >0}^{}P(1-\limsup_{n\to\infty } Yn\ge \varepsilon )$ = $\prod_{\varepsilon >0}^{}P(1-\limsup_{n\to\infty } (1-F_{Y} ))$

Stýv · 29. 05. 2020 22:58

Začalo to nadějně, ale pak ses nechala asi trochu unést… a začala páchat zločiny proti matematice. :-)

Co jsem chtěl vidět bylo $P(\forall \varepsilon >0 \exists n_{o}\forall n\ge n_{o}:Yn<\varepsilon )=1$ . Z té věty ale vyplývá $P(\dotsc)=0$ , takže je třeba udělat negaci toho výroku v závorkách - to jsi v podstatě udělala, ale $P(1-\dotsc)$ je nesmysl – mělo by to být $1-P(\dotsc)$ . Pak ses taky pokusila zbavit toho $\varepsilon$ , což je potřeba, ale ne takhle – ty jevy evidentně nejsou nezávislé, takže nejde počítat součin pstí.

Zkus se zamyslet, jestli by to nešlo "vytknout", tj. jestli tvrzení $\forall \varepsilon >0: P(\exists n_{o}\forall n\ge n_{o}:|Yn-Y|<\varepsilon )=1$ je silnější nebo slabší než $P(\forall \varepsilon >0 \exists n_{o}\forall n\ge n_{o}:|Yn-Y|<\varepsilon )=1$ .

Když to dáš dohromady, vyjde ti, že $A_n=[Y_n\geq\varepsilon]$ a stačí ověřit předpoklad Cantelliho věty.

Pomeranc · 30. 05. 2020 14:27

↑ Stýv:

Nedaří se mi ověřit předpoklad Cantelliho věty.
Pro odstranění epsilonu by šlo využít spojitost míry.
//forum.matweb.cz/upload3/img/2020-05/39773_Spojitost%2Bm%25C3%25ADry.PNG

Když jsem to upravovala došla jsem k
$P(\bigcap_{\varepsilon>0 }^{}\liminf_{n\to\infty }Yn<\varepsilon )$ = $\lim_{\varepsilon \to0_{+}}1-P(\limsup_{n\to\infty }Yn\ge \varepsilon )$

$\sum_{n=1}^{\infty }P(An^{\varepsilon })$ = $\sum_{n=1}^{\infty }1-P(min\{X1,..Xn\}<\varepsilon )$

A ty mám pochybnosti, jestli ta suma vyjde opravdu konečná.

Matematické Fórum

#1 26. 05. 2020 23:29

PAST konvergence v míře,sj

#2 27. 05. 2020 01:35

Re: PAST konvergence v míře,sj

#3 27. 05. 2020 12:49

Re: PAST konvergence v míře,sj

#4 27. 05. 2020 14:01

Re: PAST konvergence v míře,sj

#5 27. 05. 2020 22:54

Re: PAST konvergence v míře,sj

#6 28. 05. 2020 00:39

Re: PAST konvergence v míře,sj

#7 28. 05. 2020 00:54

Re: PAST konvergence v míře,sj

#8 28. 05. 2020 01:03

Re: PAST konvergence v míře,sj

#9 28. 05. 2020 01:37 — Editoval Pomeranc (28. 05. 2020 01:39)

Re: PAST konvergence v míře,sj

#10 28. 05. 2020 08:02

Re: PAST konvergence v míře,sj

#11 28. 05. 2020 13:11

Re: PAST konvergence v míře,sj

#12 28. 05. 2020 16:44

Re: PAST konvergence v míře,sj

Pomeranc napsal(a):

Pomeranc napsal(a):

#13 28. 05. 2020 20:43

Re: PAST konvergence v míře,sj

#14 28. 05. 2020 21:07

Re: PAST konvergence v míře,sj

#15 28. 05. 2020 21:16

Re: PAST konvergence v míře,sj

#16 29. 05. 2020 00:58

Re: PAST konvergence v míře,sj

#17 29. 05. 2020 14:34

Re: PAST konvergence v míře,sj

#18 29. 05. 2020 15:14

Re: PAST konvergence v míře,sj

#19 29. 05. 2020 17:17

Re: PAST konvergence v míře,sj

#20 29. 05. 2020 18:37

Re: PAST konvergence v míře,sj

#21 29. 05. 2020 18:48

Re: PAST konvergence v míře,sj

#22 29. 05. 2020 18:55

Re: PAST konvergence v míře,sj

#23 29. 05. 2020 20:01

Re: PAST konvergence v míře,sj

#24 29. 05. 2020 22:58

Re: PAST konvergence v míře,sj

#25 30. 05. 2020 14:27

Re: PAST konvergence v míře,sj

Zápatí