Matematické Fórum

mbendi · 24. 06. 2009 19:19

ahojte, mohli by ste mi niekto objasnit co je myslene tymto zadanim a ako na to?f'(x) je parcialna derivacia?
Funkcia y=f(x):R->R je urcena imlicitne rovnicou
$x^3+y^3-6xy=0$ a bodom (3,3).
Najdite vsetky body x patri R, pre ktore plati f'(x)=0.

mbendi · 24. 06. 2009 19:21 — Editoval mbendi (24. 06. 2009 20:09)

a este 2. otazka ze ako sa derivuje imlicitna funkcia 2 premennych?najskor podla x podla y a potom sa to spolu vynasobi?

mbendi · 24. 06. 2009 21:30

haloo!mozte mi to prosim vas niekto objasnit.zajtra mam skusku a takyto typ prikladu sa tam vyskytuje pomerne casto.

jelena · 25. 06. 2009 00:03 — Editoval jelena (25. 06. 2009 05:48)

Zdravím, doufám, že jsem to pochopila správně a jelikož jsem dnes měla nějaké hrubky v derivacích, tak si to dám za trest.

je mi záhadou, proč je dán bod (3, 3)

Zadání inplicitní funkce $x^3+y^3-6xy=0$ derivuji po x a pamatuji si, že y je funkce od x:

zejména součín (nebo podíl, nebo složená funkce) je zradno $(6xy)^{\prime}=(6x)^{\prime}y+6x(y)^{\prime}=6y+6x(y)^{\prime}$

$3x^2+3y^2y^{\prime}-6y-6xy^{\prime}=0$

odsud vyjádřím y´=f´(x)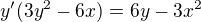

$y^{\prime}(3y^2-6x)=6y-3x^2$

$y^{\prime}=\frac{6y-3x^2}{3y^2-6x}$

máme řešit, kdy je f´(x)=0

$\frac{2y-x^2}{y^2-2x}=0$

čítatel má být nula, jmenovatel nesmí - toto bých řešila graficky>

citatel $2y-x^2=0$ upravím na $y=\frac{x^2}{2}$ je to parabola orientovana po ose y, vetve nahoru.

jmenovatel $y^2-2x\neq0$ upravim na $\frac{y^2}{2}\neq x$ to je parabola orientovana po ose x, vetve doprava.

Odpoved bude parabola $y=\frac{x^2}{2}$ bez bodů, kde se setkává s parabolou $\frac{y^2}{2}\neq x$ , to znamená bez (0, 0) a ještě jednoho průníku, kde se potkáji.

Kritika? Dekuji :-)

EDIT: nejsem si úplně jistá, ale myslím si. že zavěrem řešení má být dosazení výrazu pro povolená x: $y=\frac{x^2}{2}$ do původního zadání funkce: sem $x^3+y^3-6xy=0$ a nalezení konkrétní hodnoty x, pro kterou je splněna jak podmínka nulové derivace, tak i to, že ten bod funkce patří.
Zároveň vyloučít z oboru pro x body, co jsme vyloučili druhou podmínkou pro derivace: $\frac{y^2}{2}\neq x$ také dosadit do $x^3+y^3-6xy=0$ .

Kritika?

mbendi · 25. 06. 2009 00:39

↑ jelena:ja ti to kritizovat teda nebudem:). dakujem este si to musim par krat precitat..

jelena · 25. 06. 2009 05:49 — Editoval jelena (26. 06. 2009 00:32)

↑ mbendi:

přidala jsem EDIT do ↑ jelena:.

EDIT 2. silně expresivní :-)

je mi záhadou, proč je dán bod (3, 3)

Moji záhady, jako ostatních 99,99 % problémů, co mám, již vyřešil kolega Kondr (přesně před 2 lety) a dokonce si přesně vybavuji poznamku o ručním dokreslení křívky v okolí nuly :-)

Matematické Fórum

#1 24. 06. 2009 19:19

deriavacia f(x) v rovnici s dvoma premennymi

#2 24. 06. 2009 19:21 — Editoval mbendi (24. 06. 2009 20:09)

Re: deriavacia f(x) v rovnici s dvoma premennymi

#3 24. 06. 2009 21:30

Re: deriavacia f(x) v rovnici s dvoma premennymi

#4 25. 06. 2009 00:03 — Editoval jelena (25. 06. 2009 05:48)

Re: deriavacia f(x) v rovnici s dvoma premennymi

#5 25. 06. 2009 00:39

Re: deriavacia f(x) v rovnici s dvoma premennymi

#6 25. 06. 2009 05:49 — Editoval jelena (26. 06. 2009 00:32)

Re: deriavacia f(x) v rovnici s dvoma premennymi

Zápatí