Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 09. 2009 16:12 — Editoval lukaszh (01. 09. 2009 16:13)
Curve of pursuit
Zdravím,
už dávnejšie sa tu riešila zaujímavá úloha. Pri plávaní po internete som si na ňu spomenul a nebol som veľmi spokojný, že zostala otvorená. Úlohu som začal riešiť, ale čisto z geometrického hľadiska. Bol by som rád, keby niekto pridal ucelené riešenie k tejto úlohe, lebo ma skutočne veľmi zaujala. Podobne ako na stránkach p. Maříka, kde ťaháme psa na lane :-) Skutočne pekné využitie dif. počtu.
Začal som uvažovať nasledovne:
(1) Predpokladám, že všetky trajektórie budú mať rovnaký tvar, len budú stočené o 90 stupňov, do štvorca.
(2) Krivky umiestnim do 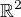 nasledovne
nasledovne
(3) Ak nájdem predpis prvej, viem aj predpisy ostatných. Označím predpis prvej krivky  nasledovne
nasledovne
Neviem teraz bližšie definovať množinu X, ale  . Podobne druhú krivku dostanem otočením prvej
. Podobne druhú krivku dostanem otočením prvej
(5) Spojnica bodov
je rovnobežná s dotykovým vektorom 
Sklon spojnice všeobecne pre t je
teda vektor, ktorý určuje jej smer je resp.
resp. 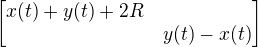
Podmienka pre trajektóriu je teda  , alfa nie je konštanta, ale ide o číslo, ktoré udáva pomer medzi dĺžkami oboch vektorov, závisí od t. Tým je vyjadrená rovnobežnosť. Prepísaním do rovníc vzniká systém dvoch dif. rovníc
, alfa nie je konštanta, ale ide o číslo, ktoré udáva pomer medzi dĺžkami oboch vektorov, závisí od t. Tým je vyjadrená rovnobežnosť. Prepísaním do rovníc vzniká systém dvoch dif. rovníc
Funkcia alfa by sa dala vyjadriť pomocou pomeru dĺžok oboch vektorov. Riešením by mala byť trajektória prvej, teda všetkých. Ide mi o kontrolu, či sú úvahy správne, alebo som niečo prehliadol.
Vďaka za názory.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#2 01. 09. 2009 20:18 — Editoval BrozekP (01. 09. 2009 20:24)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Curve of pursuit
↑ lukaszh:
Řekl bych, že je to všechno dobře.
Offline
#3 01. 09. 2009 21:05
Re: Curve of pursuit
↑ BrozekP:
Iste, vďaka za odpoveď. Asi to zostane len v rovine numerických riešení.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#4 01. 09. 2009 21:11 — Editoval BrozekP (02. 09. 2009 09:46)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Curve of pursuit
Offline
#5 02. 09. 2009 10:00
Re: Curve of pursuit
↑ BrozekP:
No paráda, vďaka za pomoc.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#6 02. 09. 2009 10:01
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Curve of pursuit
↑ lukaszh:
Dá se to lehce zobecnit pro n-úhelník, teď to řešíme v původním tématu.
Offline


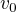 - velikostí rychlosti, která se nemění.) Ze soustavy lze snadno získat
- velikostí rychlosti, která se nemění.) Ze soustavy lze snadno získat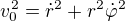 .
. ,
, (
(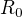 značím počáteční vzdálenost od počátku).
značím počáteční vzdálenost od počátku).