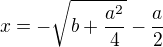Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 29. 09. 2009 19:51
Re: Rovnice
Omlouvám se, ale nechápu, kde se vezme na druhém řádku výpočtu to 0,8x
A zároveň vím, že jsem už vypadám jako debil, ale zamotal jsem se v téhle rovnici (v mocninách), nehodil byste mi někdo výpočet, abych nějak našel chybu?
Rovnice: (x-1)^3 + (x-2)^3 + (x-3)^3 = 3.(x-1).(x-2).(x-3)
Moc dík.
Offline
#5 29. 09. 2009 20:08 — Editoval Honza Matika (29. 09. 2009 20:11)
#9 29. 09. 2009 20:43 — Editoval Honza Matika (29. 09. 2009 20:56)
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Re: Rovnice
Takle se ale nic nenaučíš.
Levou stranu udělej podle vzorce (všechny 3 členy) a pravou stranu roznásob.
Pak posčítej co jde, atd. Všechno popořádku a k něčemu se dostaneš.
Edit: Mě vyšlo  , ale musíš navrhnout i své řešení
, ale musíš navrhnout i své řešení
Offline
#11 29. 09. 2009 21:09 — Editoval Honza Matika (29. 09. 2009 21:10)
#15 30. 09. 2009 09:21
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice
Zdravim vas,
jen takové doplnění (neposoudim, zda tato uloha byla zadana za ucelem procviceni mocnin, coz by byla trochu skoda, neboť trochu uzitecnejsi cesta je přes substituci prostřední závorky).

substituce a=x-2, z toho x-3=a-1, x-1=a+1 
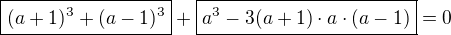 od tohoto okamziku jsem neposuzovala, zda je vhodnejsi rozklad podle vzorce
od tohoto okamziku jsem neposuzovala, zda je vhodnejsi rozklad podle vzorce 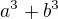 (zda se mi to lepší):
(zda se mi to lepší): 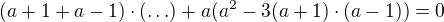
nebo takova varianta (a vytykání) 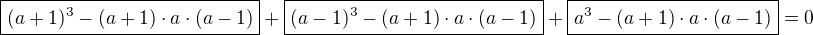 .
.
To je trochu reakce na připomínku kolegy Kondra, pozdrav :-) že malo dbame na úpravy výrazů.
Offline

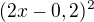 musíš si uvědomit, že je to vzorec a ten se rozkládá jako
musíš si uvědomit, že je to vzorec a ten se rozkládá jako 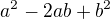
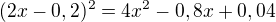
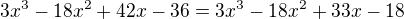

 a např.
a např. 
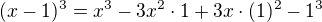
 mohu dělat následující úpravy:
mohu dělat následující úpravy: ,
,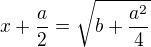 , tedy
, tedy 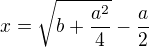
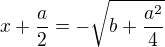 , tedy
, tedy