Matematické Fórum

frazer · 14. 01. 2010 22:55

Tak zdarvim po delsi pauze jsem tu opet.Uz se normalne bojim zdejsich moderatoru jsou to drsni chlapi.No nic ridil jsem se heslem co si neudelas sam to nemas a tak jsem se pokusil cast prikladu vyresit
Prispevek sem davam proto jestli muj chod myslenek je spravny

1. Ve vektorovem prostoru R5 se standardnim skalarnim soucinem najdete
bazi a dimenzi prostoru

{(3;-1; 0; 2; 1); (5;-2;-1; 3;-1); (3;-2;-3; 1;-7)}

Tak tyto tri vektory jsem napsal pod sebe do matice a upravil je na trojuhelnikovy tvar.Zjistil jsem ze posledni vektor je nulovy tim padem bude dimenze 2 a baze budou napriklad ty dva zbyle radky(vektory) matice, zrejme to boudou i generatory

2. Necht' endomorfizmus f : R2 --> R2 ma vzhledem k bazi {(-1; 2); (1;-3)}
matici
1 1

0 1

Overte, ze f je automorfizmus a najdete vzor vektoru (3; 4) v tomto automorfizmu.

s timhle si nevim rady

3. Ve vektorovem prostoru R4 se standardnim skalarnim soucinem najdete
ortonormalni bazi podprostoru <(0;-1; 1; 1); (3; 0;-1;-2); (-2; 2; 2; 3)> ob-
sahujici kladny nasobek vektoru (0;-1; 1; 1).

tady u tretiho prikladu bych pouzil gramm-schmidt ale nevim jak

ma nekdo nejaky navrh?

to moderator: nezlob se

Kondr · 15. 01. 2010 09:57

Myslel jsem, že přesuneme diskusi tam, kde odpovídal Olin, ale podruhé kázat nebudu.

1) Souhlasím.

2) Automorfizmus poznáme tak, že má k nějaké bázi regulární matici. O automorfizmus tedy jde. Najdeme inverzní matici k matici endomorfismu, určíme souřadnice vektoru (3,4), vynásobíme je tou inverzní maticí (zleva) a máme souřadnice hledaného vektoru.

3) Nejprve ortogonální báze. Do ní dáme (0;-1; 1; 1), následně určíme projekci (0;-1; 1; 1) na (3; 0;-1;-2) a odečteme ji od (3; 0;-1;-2) -- vyjde
(3; 0;-1;-2)+ (0;-1; 1; 1)=(3,-1,0,-1). Poslední vektor v bázi získáme tak, že od (-2; 2; 2; 3) odečteme projekce na zbylé dva vektory v bázi.
Poté co máme ortogonální bázi, vydělíme každý vektor jeho velkostí.

frazer · 15. 01. 2010 14:23

nebylo by možne to 2 a 3 nejak rozepsat? dekuji

frazer · 15. 01. 2010 15:17

k pr.2 :urcil jsem tedy inverzni matici a ted nevim jak urcit souradnice vektoru(3,4) abych to mohl vynásobit zleva tou inversni matici?
u pr 3 nechapu jak vypada zapis? dekuji vam

frazer · 15. 01. 2010 16:08

is there anybody out there ? pomozte prosim potreboval bych to na zapich dekuji vam moc

frazer · 15. 01. 2010 16:57

Kondr please

Kondr · 15. 01. 2010 17:02

Jsou-li souřadnice vektoru 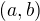$(a,b)$ , pak musí platit $a(-1; 2)+b(1;-3)=(3;4)$ . K jejich určení stačí řešit 2 rovnice o 2 neznámých. Po vynásobení inv. maticí ti vyjdou souřadnice c,d, výsledek je pak $c(-1; 2)+d(1;-3)$ .

Použití Gram-Schmidta je celkem standardní, moc nevím, jak dál poradit. Zkoušel jsem k tomu něco psát tady: http://forum.matweb.cz/viewtopic.php?id=13341

frazer · 15. 01. 2010 17:32

fain takze jsem spocetl ze pro a,b jsou souradnice(-13,-10)
inverzni matice je
1 -1 -13
0 1 krat -10

to vyslo (-3,-10) co jsou koeficiety c,d ty jsem dosadil do te rovnice a vyslo:
(-7,24) muze to tak byt?

A ted jeste nejak tu trojku.V tomhle semestru mame jen zapocet z algebry zkousku az pristi

halogan · 15. 01. 2010 21:24

(Asi budu jeden z těch drsných chlapů :-), tak tě prosím o jedno - nepiš tady prosivé příspěvky, my se ti budeme věnovat... až tu budeme.)

Kondr · 15. 01. 2010 22:29

Jen doplním, že ta čísla (-7,24) odpovídají. K trojce zkus nějak upřesnit, co není jasné -- zápis bude obsahovat nějaké skalární součiny, tak jako v odkazovaném tématu.

frazer · 16. 01. 2010 17:30

zdravim
tu trojku sem nakonec spocital podle gram-schmmidta .vcera jsem to odeslal a uvidim co mi na to rekne.az to budu mit opravene tak to sem dam dekuji vam vsem

Matematické Fórum

#1 14. 01. 2010 22:55

Baze a dimenze, endomorfismus

#2 15. 01. 2010 09:57

Re: Baze a dimenze, endomorfismus

#3 15. 01. 2010 14:23

Re: Baze a dimenze, endomorfismus

#4 15. 01. 2010 15:17

Re: Baze a dimenze, endomorfismus

#5 15. 01. 2010 16:08

Re: Baze a dimenze, endomorfismus

#6 15. 01. 2010 16:57

Re: Baze a dimenze, endomorfismus

#7 15. 01. 2010 17:02

Re: Baze a dimenze, endomorfismus

#8 15. 01. 2010 17:32

Re: Baze a dimenze, endomorfismus

#9 15. 01. 2010 21:24

Re: Baze a dimenze, endomorfismus

#10 15. 01. 2010 22:29

Re: Baze a dimenze, endomorfismus

#11 16. 01. 2010 17:30

Re: Baze a dimenze, endomorfismus

Zápatí