Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 01. 2010 20:34
Geometrická posloupnost
Dobrý den, mám příklad...
V GP s q=2 vypočítejte, kolik členů dává součet 186, jestliže poslední sčítanec je 96.
Snažil jsem se to řešit soustavou dvou rovic, ale nějak mi to nevychází, mohl by mi někdo prosím pomoci to dopočítat?

Vyjádřil jsem  , ale (pokud je to dobře) s tou neznámou v exponentu si nevím rady :-)
, ale (pokud je to dobře) s tou neznámou v exponentu si nevím rady :-)
Offline
- (téma jako vyřešené označil(a) Allo)
#4 18. 01. 2010 21:04 — Editoval Allo (18. 01. 2010 21:07)
Re: Geometrická posloupnost
Tak to právě nechápu...Vím, že je to smutný, ale já mám díry v těhle základech, třeba to vymyslim, ale jak je tam mocnina, jsem v háji...
z první rce vyjádřím 
dosadím do první a mám 
a nevím, jak z toho osamostatnit n...tuším, že se tam nějak používá logaritmus, ale nejsem schopný to nějk upravit
Offline
#5 19. 01. 2010 00:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometrická posloupnost
součet:  , odsud
, odsud  dosazuji do vzorce pro n-tý člen
dosazuji do vzorce pro n-tý člen
n-tý člen ,
,
máme rovnici: levou a pravou stranu násobím
levou a pravou stranu násobím 
 teď budou úpravy, pokud některá není jasná, tak dej vědet.
teď budou úpravy, pokud některá není jasná, tak dej vědet.




 , odsud
, odsud 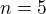
Může být?
Offline


 zbytek zvládneš
zbytek zvládneš