Matematické Fórum

hollowback

Zdravim, mam nejaky takovy priklad
Tři děti si z krabice vytáhli 6 hraček. Kolika způsoby se o ně mohou podělit tak, aby každé dítě mělo alespoň jednu hračku?

Mame 6 hracek a 3 deti. Na zacatku aby kazde dite melo jednu hracku si je rozdelim takto o|o|o. Nyni nam zbyvaji 3 hracky, ktere musime rozdelit mezi dve deti. Takze si to rozdelim na 3 hracky a dve |. Pouziji kombinaci (3+2) nad 2, takze 5 nad 2. Vysledek je 10 moznosti.

Je toto spravne reseni?

musixx · 14. 01. 2009 15:59 — Editoval musixx (14. 01. 2009 16:09)

↑ hollowback: Predpokladam, ze neni jedno, jestli napr. dite1 dostane hracku1, dite2 hracku2 a dite3 zbyle 4 hracky, nebo jestli dite1 dostane hracku2, dite2 hracku1 a dite3 zbytek. Tzn. ze bych predpokladal, ze deti i hracky jsou mezi sebou vzajemne rozlisitelne. Takze to rozhodne dobre nemas.

Ja bych na to sel takto:

1. Deleni hracek v pomeru 1:1:4, tedy vyberu dite, ktere dostane 4 hracky --> 3 zpusoby. Pak mu vyberu 4 hracky --> $6\choose4$ zpusoby. Pak zbyle 2 hracky rozdelim mezi zbyle deti --> 2 zpusoby. Celkem ma tato prvni moznost $3\cdot{6\choose4}\cdot2=90$ moznosti.

2. Deleni hracek v pomeru 1:2:3, tedy vyberu dite, ktere dostane 3 hracky, pro nej $6\choose3$ moznosti pro vyber hracek, pak vyberu ze zbylych 2 deti to, ktere dostane 2 hracky --> 2 zpusoby a vyber ze zbylych 3 hracek --> $3\choose2$ . Celkem tedy $3\cdot{6\choose3}\cdot2\cdot{3\choose2}=360$ moznosti.

3. Deleni 2:2:2, ted pozor, at neco nezapocitame dvakrat! Dam hracky do rady --> 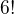$6!$ zpusobu. Deti jiz nesetrizuji, protoze prvni dve hracky dam prvnimu diteti, druhe dve druhemu a treti dve tretimu. Nezalezi na tom, v jakem poradi konkretni dite hracky dostane, tedy mohu prehodit 1. a 2. hracku (2 zpusoby), i 3. a 4. (opet 2 zpusoby) i 5. a 6. hracku. Celkem tedy $\frac{6!}{2^3}=90$ moznosti.

Jine deleni hracek neexistuje. Tedy vsech moznosti je 90+360+90=540.

hollowback · 14. 01. 2009 16:49

Dobre diky.
Jeste mam jeden problem :)
17 různých úloh na 2 současně pracujících PC.JAk je možné úlohy rozdelit mezi tyto 2 pc, aby každý zpracovaval alespon jednu úlohu
Melo by se to resit podobne jako ty hracky nebo je na to jeste jiny zpusob??

musixx · 14. 01. 2009 16:52

↑ hollowback: Je to mozne resit jako ty hracky, ale bylo by to hodne moznosti. Coz takhle to spocitat tak, ze nejprve nebudes uvazovat podminku, aby kazdy pocitac resil aspon jednu ulohu. A na zaver odectes 2, protoze jsou prave dve moznosti, ze vsechno resi jeden pocitac. Doufam, ze takova napoveda staci.

hollowback · 14. 01. 2009 17:04

Jj, staci to....diky :)

Kondr · 14. 01. 2009 17:06

K hračkám: možno postupovat i naopak: pro každou hračku se rozhodneme, komu ji dáme: 3^6 možností. Odečteme možnosti, kdy jedno dítě nic nedostalo: 3*2^6 možností. Stavy, kdy všechno dostalo jedno dítě jsme odečetli dvakrát, jednou je přičteme: 3 možnosti.
729-192+3=540.

Podobně u počítačů: 2^17 možností, jak úlohy rozdělit, odečteme dvě, kdy všechno zpracovává jeden stroj.

Samot · 27. 01. 2010 13:44

Já bych se chtěl taky ještě dotázat. Máme příklad kdy:

Sněhurka má za úkol uložit 12 čepiček do dvou šuplíku a podmínka je, aby v každém šuplíku byly alespoň 3 čepičky

Princip řešení je asi stejný že? děkuji

Kondr · 27. 01. 2010 14:33

↑ Samot: Ano, je.

Bobes · 27. 01. 2010 14:38

↑ Samot:
Podle mne to neni stejne, protoze v zadani bylo jeste pripsano ze vsechny cepicky jsou stejne. Proto si myslim ze staci dat do tech dvou supliku po 3 cepicky a potom je uz jenom 7 moznosti jak je rozdelit a to tak ze z tech zbylych je v prvnim 6 v druhem 0 nebo 5 a 1 nebo 4 a 2. => to plati i naopak a pak jeste moznost kdy jsou 3 a 3. Dohromady to dava 7 moznosti

Kondr · 27. 01. 2010 14:48

↑ Bobes: Pokud bylo zadání takto, pak ano. Ale tato verze mi připadá tak pro druhou třídu, kde se počítají úlohy typu "kůly v plotě jsou metr od sebe, kolik kůlů potřebujeme na šestimetrový plot". Není v tom zadání ještě nějaká informace?

Samot · 27. 01. 2010 14:57

To, že jsou stejné jsem přehlédl, klasická chyba. Tady je celé zadání:

Sněhurka bydlí u 12 trpaslíků. Chce uložit jejich 12 stejných čepiček do dvou šuplíků. Kolika způsoby to může provést, pokud chce, aby v každém šuplíku byly alespoň 3 čepičky.

andross · 27. 01. 2010 14:58

↑ Kondr: zadani je: Snehurka bydli u dvanacti trposu. Chce ulozit jejich 12 stejnych cepic do dvou supliku. Kolika zpusoby to muze provest, pokud chce, aby v kazdem supliku byly alespon 3 cepky

petrkovar · 28. 01. 2010 21:47

↑ hollowback:Shrnutí:
V druhé kapitole jsme řešili několik základních typů úloh. U všech těchto příkladů stačí poznat, která typovka to je.
- Úloha hračky spadá mezi nalezení všech surjekcí mezi dvěma množinami. Obecně jsme ji řešili na cvičeních. Početní postup pak odpovídá tomu, co psal Kondr. Vysvětlení bych pak viděl postavení spíš na principu inkluze a exkluze.
- Úloha PC je ta nejjednodušší varianta ze sady zadání, kdy máme jen 2 počítače a na každém má běžet alespoň jedna úloha. Pokud by bylo počítačů více (a byly různé, což jsme v zadání požadovali), tak se úloha bude řešit stejně jako hračky. Proč?
- Úloha s trpaslíky (zase jste vybrali tu nejlehčí ze šesti variant. Pokud by šuplíků bylo více, bude se postupovat JINAK, než u předchozích dvou typovek, protože čepičky jsou stejné. Jedná se o typovku s rozdělením čísla na sčítance s tím, že rozlišujeme pořadí sčítanců (bylo na dnešní písemce).
Další typovky mám rozebrané v přednáškách na webu.

petrkovar · 28. 01. 2010 21:49

↑ Kondr:Bojím se, že bychom dostali nezanedbatelné procento šestek. Proto píšu i tuto poznámku.

Matematické Fórum

#1 14. 01. 2009 15:56 — Editoval hollowback (14. 01. 2009 15:57)

[DIM]Kombinatorika - rozdeleni hracek detem

#2 14. 01. 2009 15:59 — Editoval musixx (14. 01. 2009 16:09)

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#3 14. 01. 2009 16:49

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#4 14. 01. 2009 16:52

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#5 14. 01. 2009 17:04

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#6 14. 01. 2009 17:06

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#7 27. 01. 2010 13:44

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#8 27. 01. 2010 14:33

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#9 27. 01. 2010 14:38

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#10 27. 01. 2010 14:48

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#11 27. 01. 2010 14:57

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#12 27. 01. 2010 14:58

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#13 28. 01. 2010 21:47

Re: [DIM]Kombinatorika - rozdeleni hracek detem

#14 28. 01. 2010 21:49

Re: [DIM]Kombinatorika - rozdeleni hracek detem

Zápatí