Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyšetřete spojitost funkce 2 proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 01. 2018 20:37
- dominiksep
- Příspěvky: 54
- Reputace: 0
Vyšetřete spojitost funkce 2 proměnných
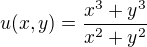
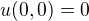
Vyšetřete spojitost.
Zatím jsem spočítal  , mám tedy kandidáta na limitu, který neodporuje hodnotě funkce. Poté jsem se pokusil limitu dokázat:
, mám tedy kandidáta na limitu, který neodporuje hodnotě funkce. Poté jsem se pokusil limitu dokázat: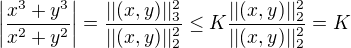
Kde nerovnost plyne z ekvivalence norem.
To mě vedlo k myšlence, že limita asi nebude konvergovat. To by se mělo dát dokázat z Heineho věty, ale nejsem schopen najít vybranou posloupnost, která by šla k něčemu jinému než k nule.
Díky.
Offline
- (téma jako vyřešené označil(a) dominiksep)
#3 19. 01. 2018 12:35 — Editoval Marian (19. 01. 2018 12:36)
Re: Vyšetřete spojitost funkce 2 proměnných
Z definice spojitosti funkce dvou proměnných je zřejmé, že stačí dokázat, že pro každé epsilon > 0 existuje prstencové delta-okolí bodu (0,0) takové, že pro všechny jeho body (x,y) platí |u(x,y)-u(0,0)| < epsilon.
K tomu si ovšem stačí rozmyslit platnost nerovnosti
ze které již plyne spojitost funkce v daném bodě. Aparát limit není nezbytný.
Offline
#4 19. 01. 2018 14:38
- dominiksep
- Příspěvky: 54
- Reputace: 0
Re: Vyšetřete spojitost funkce 2 proměnných
↑ Stýv:
Díky, teď už to sedí. Limita je tedy 0.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyšetřete spojitost funkce 2 proměnných (TOTO TÉMA JE VYŘEŠENÉ)

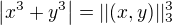 ? Odhadem byhc řekl, že to konvergovat bude, protože v čitateli jsou obě proměnné ve vyšší mocnině než ve jmenovateli.
? Odhadem byhc řekl, že to konvergovat bude, protože v čitateli jsou obě proměnné ve vyšší mocnině než ve jmenovateli.