Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vícenásobný integrál - objemy (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 07. 2009 18:17
Vícenásobný integrál - objemy
Zadání:
Vypočítejte hmotnost tělesa, které je ohraničenné rovinou z = 2 a plochou 
je-li hustota h tělesa v bodě (x,y,z) rovna h(x,y,z) = z.
Tedy:
Nejdřiv vypočítám objem daného tělesa.
Když dám do rovnosti plochy: z = 2 a  čili:
čili: 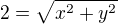
z toho tedy usoudím že průmětem bude tedy kružnice o poloměru 2, tedy objem bude asi následující: , čili vyjde mi reálné číslo.
, čili vyjde mi reálné číslo.
Jak tedy vypočítám celkovou hmotnost když h(x,y,z)=z ??? díky moc .....
Offline
#2 05. 07. 2009 00:51
Re: Vícenásobný integrál - objemy
Dle mého názoru ti objem na nic není, hmotnost prostě zjistíš integrováním hustoty přes celé těleso.
Offline
#4 06. 07. 2009 17:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vícenásobný integrál - objemy
↑ h4ck3r001:
Zdravím,
kopírováno odsud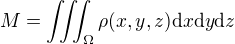 , což dle tvého zadání:
, což dle tvého zadání: 
Myslím si, že meze budou takto: - ohledně průmětu na kružnici souhlasím, z se mění od tohoto průmětu v rovině xOz až do z=2. y od je v mezích +/- \sqrt{4-x^2} (také odečteno z kružnice), x je v mezích od -2 do 2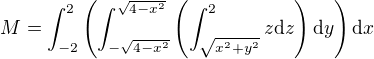
pro výpočet bude potreba prevadet do polárních souřadnic: ,
,  ,
,  ,
, 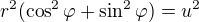 ,
,
r je v mezich od 0 do 2,  je v mezich od 0 do
je v mezich od 0 do  , u je v mezich r az 2
, u je v mezich r az 2
Jiná varianta, nad kterou jsem uvažovala, že vnější integral bude po dz, v tomto případě z se mění od 0 do 2 a vnitřní dvojný integral po dxdy by měl být obsah kruhu v průmětu, ale nějak se mi nedaří dotahnout tento nápad do rozumného závěru, tak nic.
OK?
Doufám, že někdo z kolegů zkontroluje a zkritizuje, děkuji :-)
Offline
#5 06. 07. 2009 17:39
Re: Vícenásobný integrál - objemy
↑ jelena:
oka vsechno mi sedi i vzorec pro samotny M i vsechny jeho meze, akorat sem nak nepobral prevody do polarnich souradnic, nejde to vypocitat i tak ze nebudu zadny prevody pouzivat a proste to zintegruju postupne nejdriv zintegruju podle z pak podle y a nakonec podle x, podle prislusnych mezi .. jde to taky tak??
Offline
#6 06. 07. 2009 17:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vícenásobný integrál - objemy
↑ h4ck3r001:
ale samozřejmě, jak umíš (korektně, hlavně), tak počítej - já bych se také vyhla převodu do polárních souřadníc, pokud je možnost. Můžeš poslat k výpočtu i sem: http://www.wolframalpha.com/ pro kontrolu.
Pro mne byla zajimavejší ta "jiná varianta", kterou jsem jen naznačila, zdá se mi, že by byla jednodušší co do funkcí a do mezi (počítame totiz hmotnost kuželu s proměnnou hustotou) a tak jsem si myslela, že funkce sestavena přes trojuhelník v řezu by byla jednodušší), ale nějak se to nedařilo, tak jsem přestala nad touto variantou uvažovat. Třeba někdo z kolegů.
Ať se daří.
Offline
#7 06. 07. 2009 20:17
Re: Vícenásobný integrál - objemy
↑ jelena:
Nazdar,
vzhledem k tomu, že jsem se vícerozměrnými integrály zaobíral už docela dávno (a jen letmo), nechtěl jsem na původní dotaz odpovídat konkrétním výpočtem, protože jsem se obával blbostí. Teď jsem se na to ale vrhl.
Pozor, nejedná se o polární souřadnice (ty jsou v rovině), ale o cylindrické (teď asi musím působit jako strašný hnidopich). Jakobián transformace do cylindrických souřadnic je jenom r, což nám dost usnadní výpočet.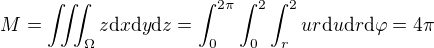 .
.
Mathematica potvrzuje:
Code:
In[1]:= Integrate[
z Boole[z^2 >= x^2 + y^2], {x, -2, 2}, {y, -2, 2}, {z, 0, 2}]
Out[1]= 4 \[Pi]Offline
#8 06. 07. 2009 23:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vícenásobný integrál - objemy
↑ Olin:
Zdar :-)
tady popisuji, jak jsem se věnovala zde řešenému problému.
nejedná se o polární souřadnice (ty jsou v rovině), ale o cylindrické (teď asi musím působit jako strašný hnidopich).
už jsem si zvykla :-) "Polární" - měla jsem na mysli x, y v rovině xOy, děkuji za opravu.
------------
83 процента всех дней в году начинаются одинаково: звенит будильник.
Offline
#9 07. 07. 2009 00:07
Re: Vícenásobný integrál - objemy
↑ jelena:
Dobré ráno :-D
Já bohužel rusky neumím vůbec nic, takže jsem z toho vlastně nic nepochytil. Jinak problematika vícerozměrných integrálů je jakž takž shrnuta v Rektorysovi jedničce, i když zrovna cylindrické souřadnice tam tuším chybí.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vícenásobný integrál - objemy (TOTO TÉMA JE VYŘEŠENÉ)