Matematické Fórum

Peter_CSR · 31. 01. 2018 08:33

Rumburak napsal(a):
↑↑ misaH:

No uvidíme. Napsal jsem mu příklad na důkaz, že $\lim_{x \to a} f(x) = L$ ,
klidně s ním proberu i příklad na důkaz, že $\neg(\lim_{x \to a} f(x) = L)$ ,
když bude mít zájem a takový příklad (přiměřeně jednoduchý) si vymyslí .

Ahoj,

tak budem teda moc vďačný ak ukážeš nejaký názorný dôkaz 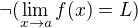$\neg(\lim_{x \to a} f(x) = L)$ . Vymysli si prosím nejaký príklad, ktorý sám považuješ za zaújmavý (nemusí byť úplne jednoduchý, tvoje poznámky boli triviálne, som si istý, že zvládnem aj viac).

Ďakujem :)

Rumburak

↑ Peter_CSR:

Ahoj.

Pro maximální názornost vezměme příklad velmi jednoduchý: dokažme, že

(1) $\neg(\lim_{x \to \pi} \sin x = 2)$ .

Budeme postupovat sporem. Předpokládejme, že (1) neplatí. Pak ovšem musí platit

(2) $\lim_{x \to \pi} \sin x = 2$ .

To podle definice limity dále znamená, že ke každámu $\varepsilon > 0$ existuje $\delta > 0$
(obecně závisející na $\varepsilon$ ) takové, že pro libovolné $x$ splňující

$x \ne \pi$ a zároveň $-\delta < x - \pi < \delta$

bude

(3) $-\varepsilon < \sin x - 2 < \varepsilon$ .

Nerovnost (3) přepišme do ekvivalentního tvaru

(4) $2-\varepsilon < \sin x < 2 +\varepsilon$

a přpomeňme, že $\varepsilon$ má být libovolné kladné číslo. Zvolme $\varepsilon = 0,5$ . Z (4) pak
dostaneme

(5) $1,5 < \sin x < 2,5$

Avšak nerovnice (5) není splněna pro žádné reálné $x$ . To znamená, že k číslu $\varepsilon = 0,5$
dotyčné $\delta > 0$ z výše uvedené úvahy neexistuje. Tím jsme - podle definice limity -
obdrželi spor s tvrzením (2), čímž dokázáno (1).

PS. Tento jednoduchý příklad jsem vzal proto, aby podstata důkazu nebyla zastíněna
nějakými složitými početními postupy. Ale zamozřejmě by se daly nalézt příklady méně
jednoduché.

Peter_CSR

Rumburak napsal(a):
↑ Peter_CSR:

Ahoj,

ďakujem za vysvetlenie, ale nie som si istý, či rozumiem.

Čo keby som vzal príklad $\lim_{x \to \pi} \sin x = 0,1$ . To by som našile x, ktoré podľa (5) kroku by vyhovovalo nerovnici, ale pre dostatočne "malé" ε by asi nevyhovovalo Cauchyho tvrdeniu.

Alebo limita

$\lim_{x \to 1} \arcsin x = 3.1415926535897932384626433$
(zľava)

Aké ε by som hľadal, aby som vyvrátil tvrdenie?

...existuje nejaká obecnejšia metóda, ktorá by sa dala použiť bez ohľadu na veľkosť nepresnosti výsledku limity? Ktorá nie je založena na typovaní čísla?

Snáď to dáva zmysel.

Rumburak

↑ Peter_CSR:

Ahoj.

Ano. Příklady, které uvádíš, patří právě k oněm složitějším, kde to již tak triviální není.

Mimochodem: \lim_{x \to \Pi } \arcsin x nemá smysl, protože funkce arcsin není definována
na žádném prstencovém okolí bodu "\Pi", takže základní předpoklad k tomu, abychom mohli
o uvedené limitě hovořit, není splněn.

Dále:

- Funkci "ascsin x" lze zavést integrálem s horní mezí x a takový integrál je spojitou funkcí
proměnné x.

(Víme-li , že funkce je v daném bodě spojitá, pak její limita v tomto bodě je rovna její
funkční hodnotě v tomtéž bodě a naopak . To je jedna ze základních vět matematické
analýzy.)

- Funkci "sin x" lze definovat součtem nekonečné mocninné řady v proměnné x konvergující
pro každé reálné x a každá taková řada je spojitou funkcí proměnné x.

- Při středoškolské definici goniometrických funkcí lze pomocí geometrických úvah opírajících se
o porovnání obsahů jistých obrazců ukázat, že

(1) $\lim_{x \to 0} \frac{\sin x}{x} = 1$ .

Přímo z definice limity plyne, že $\lim_{x \to 0} x = 0$ . Odtud a z (1) pak dostáváme
$\lim_{x \to 0} \sin x = 0$ , což znamená, že funkce sinus je spoljitá v 0 (neboť tam limita je
rovna funkční hodnotě). Pomocí vzorců

sin(a + b) = ... , cos (a + b) = ... , $\sin^2 t + \cos^2 t = 1$

lze pak dokázat spojitost funkce sinus (a také kosinus) i v ostatních bodech reálné osy.

Máš-li o tyto oblasti matematiky vážnější zájem, pak si sežeň příslušnou odbornou literaturu
na téma "základy matematické analýzy", "základy diferenciálního počtu" a pod.
Přes slovenskou literaturu přehled nemám, v české literatuře je klasikou tohoto žánru dílo
Vojtěcha Jarníka. Jeho knihy Diferenciální počet I., II. a Integrální počet I, II. jsou k nahlédnutí
a možná i ke stažení na webu, pokd vím. Tvé otázky jsou řešeny zejména v DI.

Matematické Fórum

#26 31. 01. 2018 08:33

Re: Pomoc s výpočtom limity

Rumburak napsal(a):

#27 31. 01. 2018 11:36 — Editoval Rumburak (31. 01. 2018 14:46)

Re: Pomoc s výpočtom limity

#28 31. 01. 2018 14:51 — Editoval Peter_CSR (31. 01. 2018 15:31)

Re: Pomoc s výpočtom limity

Rumburak napsal(a):

#29 31. 01. 2018 16:19 — Editoval Rumburak (31. 01. 2018 16:23)

Re: Pomoc s výpočtom limity

Zápatí