Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 01. 2018 19:33
Pomoc s výpočtom limity
Dopredu ďakujem všetkým, čo si nájdu čas mi poradiť:
https://imgur.com/a/nYoj7
neporozumel som tomu.
Chápem, že pre každé zadané epsilom hladáme delta. Upravím nerovnosť s epsilonom a na základe toho určím deltu. /všetko po bod b) som pochopil, ale v bode c) mi nie je jasné odkiaľ prišli k nerovnosti 7/3 - 1/300 > 2 a teda nechápem ani záverečnému tvrdeniu.
Ďakujem moc!
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#2 23. 01. 2018 19:57
Offline
#3 23. 01. 2018 19:59
Offline
#4 23. 01. 2018 20:58
Re: Pomoc s výpočtom limity
....premýšlal som nad tým celým a uvedomil som si, že chápem celý príklad zle...
Plz., predpokladajte že som blebeček a ako takému mi príklad vesvetlite...
Ďakujem... :/
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#5 24. 01. 2018 13:33 — Editoval Rumburak (24. 01. 2018 13:34)
Re: Pomoc s výpočtom limity
↑ Peter_CSR:
Ahoj.
Je potřeba neplést si dvě věci:
1) vypočítat vhodnou technikou hodnotu limity, pokud limita existuje,
2) na základě definice limity rozhodnout, zda dané číslo limitou je či není.
V přiloženém textu je na příkladu probrán bod 2. Možná je ten příklad pro "začátečníka
v limitách" příliš složitý. Zkus se zamyslet nad příkladem jednodušším:
Z definice limity dokažte, že
a)  ,
,
b) není pravda, že 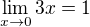 .
.
Offline
#6 24. 01. 2018 21:53 — Editoval Peter_CSR (25. 01. 2018 01:28)
Re: Pomoc s výpočtom limity
↑ Rumburak:
Ahoj! :)
A ďakujem moc za tvoj čas :).
Uhm...nie som až tak úplne začiatočník v limitách, iba som hrrrrooozne moc zabudol :D .
Každopádne, pokiaľ ide o a) riešil by som:
Zadám ľubovoľné Epsilon a tvrdím, že nájdem Delta také, že pre každé x nachádxajúce sa v intervale (a - delta,a + delta) (a je bod kde hladám limitu), bude platiť, že f(x) sa bude nachádzať v intervale (L -Epsilon, L + Epsilon), kde L je limita v bode a.
Toľko k teórií :)
Takže pre Epsilon = 1
abs(2x - 0) < 1 a abs(x - 0) < Delta a teda abs(x) < 1/2.... Takže Delta je 1/2 v tomto prípade....
Ak zadám Epsilon = 1/2, rovnakou cestou ukážem že Delta je 1/4.
....teraz asi budem potrebovať použiť matematickú indukciu (ajaj :D ) a ukázať, že pre postupnosť Epsilonov napríklad ɛ_{n} = 1/n, n ide do nekonečna, nájdem postupnosť pre δ_{n} = 1/2n a táto postupnosť bude platiť pre pre každé ďalšie n+1...
....takže, ako som už ukázal...
ɛ_{1} = 1/1, δ_{1}= 1/2
ɛ_{2}= 1/2, δ_{2} = 1/4
ɛ_{3} = 1/3, δ_{3} = 1/6
ɛ_{4} = 1/n,δ_{4} = 1/2n
....aehem.... "je triviálne dokázať, že vzťah skutočne platí a že pre ɛ_{n + 1} = 1/(n+1) je δ_{n + 1} = 1/2(n+1) a pozorný čiťateľ si dokončí dôkaz vo svojom voľnom čase"
- Každá Učebnica Matematiky Na Svete
:D :D :D :D
Takže, ako si čitateľ "dokázal" že nachádzame postupnosť, stačí už len ukázať, že limita (f(a) + ɛ_{n}) = limita (f(a) - ɛ_{n}) a pretože f(a) je 0 a ɛ_{n} sa limitne blíži k 0, je dokaz dokončený.
:D :D :D
b) Ako sme v a) prekázali, lim f(a) =0 a teda dôkaz sporom, ak tvrdím že lim f(x) = 1, musí sa lim (+ -ɛ_{n} + f(a)) = 1 pre lim δ_{n} ale f(a) = 0 a lim ɛ_{n} = 0, čo je spor, a teda Quod Erat Demonstrandum.
:D :D :D
Robím si srandu, netuším čo som práve napísal :'(
Prosím o pomoc https://imgur.com/a/HH9ZB
EDIT : práve som si uvedomil, že b) poríklad je iná funkcia, ale postupoval by som rovnako, ukázal by som, že limitou je 0 a následne sporom ukázal, že ak je 0, nemôže byť 1....
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#7 24. 01. 2018 22:12 Příspěvek uživatele Peter_CSR byl skryt uživatelem Peter_CSR. Důvod: blbosť :D
#8 25. 01. 2018 01:16
Re: Pomoc s výpočtom limity
...premýšlam (len tak pragmaticky) že je asi sprostoť tvrdiť že "funkcia je v bode a spojitá a ja vypočítam jej limitu tak, že ti poviem jej funkčnú hodnotu v a tú znepresním ju o +-ɛ, ale matematicky by to malo byť korektné a odpoveď na otázku ktorá mi bola položená :D
Každopádne ma odpoveď v učebnici nejak neuspokojila, pretože v predchádzajúcom príklade limitu "dokázali" tak, že našli proste 3 ɛ pre ktoré našli 3 δ a tvrdili "yop, takto by to bolo pre všetky prípady". 3 sú o dosť menej než nekonečne veľa... :D
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#9 25. 01. 2018 11:38 — Editoval Rumburak (25. 01. 2018 11:39)
Re: Pomoc s výpočtom limity
↑ Peter_CSR:
Ještě se k tématu vyjádřím podrobněji (snad dnes odpoledne), prozatím se koukni sem
(definice limity podla Cauchyho). Takto pojatá definice mi připadá srozumitelnější než ta,
o kterou se opíráš Ty, i když je s ní ekvivaletní.
Offline
#10 25. 01. 2018 13:02 — Editoval Rumburak (25. 01. 2018 14:24)
Re: Pomoc s výpočtom limity
↑ Peter_CSR:
Nejprve poznámka:
Pokud víme, že funkce je v daném bodě spojitá, pak její hodnota v tomto bodě bude
zároveň její limitou, stačí porovnat definici spojitosti funkce v bodě s definicí její vlastní limity
v tomto bodě.
Příklad k hlavnímu tématu:
Uvažujme funkci  pro
pro  (tj. její případná hodnota v nule
(tj. její případná hodnota v nule
nás vůbec nezajímá) a dokažme, že 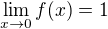 . Postupujme podle Cauchyho
. Postupujme podle Cauchyho
definice.
Nechť  (s "abstraktní" podobou předpokladu nutno vystačit). Hledáme
(s "abstraktní" podobou předpokladu nutno vystačit). Hledáme 
(obecně závisející na  ) takové, aby pro libovolné
) takové, aby pro libovolné  platilo
platilo
(1)  .
.
Odtud úpravami
 ,
,
 ,
,
 ,
,
(2)  .
.
Všimni si, že nerovnici (2) jsme z nerovnice (1) zíslkali pouze ekvivalentnímí úpravami
(za výše uvedeného předpokladu  ), takže také z (2) pak plyne (1). Nyní stačí v (2)
), takže také z (2) pak plyne (1). Nyní stačí v (2)
položit 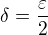 (je zřejmé, že
(je zřejmé, že  ).
).
Ukázali jsme:
K libovolně danému  lze nalézt
lze nalézt  (např.
(např. 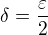 ) takové, že pro llbovolné
) takové, že pro llbovolné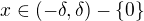 platí
platí  .
.
Pole Cauchyovy definice vlastní limity ve vlastním bodě to znamená, že
 .
.
Obecnější případ vlastní limity v nenulovém vlastním bodě je jen o málo složitější a lze ho
případně snadno zvládnout substitucí.
Offline
#11 25. 01. 2018 21:04 — Editoval Peter_CSR (26. 01. 2018 00:50)
Re: Pomoc s výpočtom limity
↑ Rumburak:
hmm.... rozumiem... rozumiem... vcelku triviálne, až na...
Čo keby som teda chcel dokázať, že lim f(x) = 2x + 1 = 2, pre x idúce k 0. Všetko by šlo okey-dokey až k (2), kde chcem osamostatniť x....
Dostal by som:
takže z toho plynie:
zadám 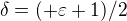
Voľným okom môžme vidieť, že sa delta nikdy nedostane k 1/2 alebo nižšie.
takže, tento dôkaz vidím ako korektný podľa Cauchyho (pre každé ε skutočne nájdeme δ), ale Žabiak Pepe má k tomu ostré výhrady: δ musí byť ľobovoľne malé, čo nie je (Pepeho indukčný dôkaz o postupnosti δ(n) limitne sa blížiacej k nule...)
Takže neviem... Kde je chyba...? O.o
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#12 25. 01. 2018 21:11 — Editoval Peter_CSR (25. 01. 2018 22:15) Příspěvek uživatele Peter_CSR byl skryt uživatelem Peter_CSR.
#13 25. 01. 2018 21:14 Příspěvek uživatele Peter_CSR byl skryt uživatelem Peter_CSR. Důvod: blbosť
#14 26. 01. 2018 00:52
Re: Pomoc s výpočtom limity
...pozerám na to a stále ma nenapadá... Problém vidím tu: " k libovolnému reálnému číslu epsilon kladnému existuje takové delta kladné". Keby to bolo opačne, bolo by to hotové: nenájdem ľubovoľné delta, ale takto...
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#15 26. 01. 2018 01:10 — Editoval misaH (26. 01. 2018 01:14)
- misaH
- Příspěvky: 13460
Re: Pomoc s výpočtom limity
↑ Peter_CSR:
Stačilo by, keby si si to nakreslil...
Ak je skutočná limita 2, tak sa dá celá situácia ľahko znázorniť a odargumentovať. Pre veľmi malé epsilonové okolie "limity" vhodné delta okolie ixu už nenájdeš.
Mimochodom, tvoje delta okolie nemá podobu
-delta < x < delta
Offline
#16 26. 01. 2018 01:27
Re: Pomoc s výpočtom limity
↑ misaH:
presne tak. Napadlo ma to práve teraz.
opravím sa zajtra, už je neskoro.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#17 26. 01. 2018 22:21 — Editoval Peter_CSR (26. 01. 2018 22:34)
Re: Pomoc s výpočtom limity
misaH napsal(a):
↑ Peter_CSR:
Stačilo by, keby si si to nakreslil...
Ak je skutočná limita 2, tak sa dá celá situácia ľahko znázorniť a odargumentovať. Pre veľmi malé epsilonové okolie "limity" vhodné delta okolie ixu už nenájdeš.
Mimochodom, tvoje delta okolie nemá podobu
-delta < x < delta
už mi z toho začína kvapkať na karbid.
Deltové okolie je správne znázornené. To, že je to neplatné tvrdenie, je zamozrejmé, zámerne som také vybral. Nenapadá ma ako svoje tvrdenie všeobecne, mohol by som vziať ε = 0.1 , dosadiť do δ = (0.1 + 1)/2 a vziať x = -1/2 a overiť že abs(f(x) - L) > ε čo je spor s Cauchym, ale to sa mi nezdá, je to základoškolský postup dosadzovaním čísielok, treba to zapísať poriadne... napíšem Rumburakovi....
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline
#18 29. 01. 2018 14:00
Re: Pomoc s výpočtom limity
↑ Peter_CSR:
Ahoj.
Tvoji zprávu jsem zaznamenal, ale bohužel se mi ztratila.
Také nevím, ke kterému konkretnímu příkladu se Tvá posledné prosba vztahuje.
Můžeš ho připomenout ?
Offline
#21 29. 01. 2018 15:24 — Editoval misaH (29. 01. 2018 15:25)
- misaH
- Příspěvky: 13460
Re: Pomoc s výpočtom limity
↑ Rumburak:
:-)
Zadávateľ evidentne nerozumie...
Napíšem, že nemá delta okolie (-delta, plus delta) - on napíše, že má.
Píše o delte, ako keby išlo o epsilon...
Dôkaz sporom považuje za nejaký pofidérny ZŠ postup...
Tak dúfa, že ty mu pomôžeš :-)
Osobne si myslím, že zadávateľ sa len tak hrá a vlastne mu o nič nejde...
Offline
#24 29. 01. 2018 21:05
Re: Pomoc s výpočtom limity
:D :D :D
Ahoj, čítam vašu konverzáciu. Ešte popremýšlam nad poznámkami MisiH a pokúsim sa svoju otázku zformulovať jasne a presne. :)
Za prípadnú neprehľadnosť threadu sa ospravedlňujem.
2 + 2 is 4 minus 1 thats 3 quick mafs.
Offline

 ,
, 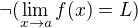 ,
,