Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé a náročnější úlohy z fyziky
- » Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
#1 13. 03. 2018 11:23 — Editoval Andrejka3 (13. 03. 2018 11:30)
Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
Ahoj.
Mám těleso, které vznikne z krychle odřezáním všech jejích rohů (v půlkách hran). Zajímalo by mě, jak by se dala vypočítat pravděpodobnost, že po náhodném hodu padne trojúhelník (stojí na trojúhelníkové stěně).
Máte nějaký nápad (kromě dostatečně mnohokrát opakovaného pokusu :D )?
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 13. 03. 2018 12:20 — Editoval Andrejka3 (13. 03. 2018 13:07)
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
↑ Ferdish:
Ráda bych to přiblížila skutečnosti. Myslím, že nejsou rovnocenné.
Možná by mohlo mít smysl uvažovat situaci, kdy kostka leží na hraně, projít úhly náklonu a dívat se, kde je těžiště -- kam se to převáží (mi poradil kamarád)(?)
Edit: Pokud je ta kostka právě postavená na hranu a má nulovou rychlost, pak s 64% pravděpodobností spadne na čtverec. viz Wolfram
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 13. 03. 2018 14:56 — Editoval Ferdish (13. 03. 2018 14:56)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
Tak samozrejme, v prípade nerovnocennosti bude treba uvažovať polohu ťažiska a veľkosti uhlov naklonenia.
V tom prípade ale (aby sme sa naozaj priblížili skutočnosti) bude treba okrem prípadu, kedy teleso leží na hrane, uvažovať aj prípad, kedy kocka bude balansovať na vrchole...
Offline
#5 14. 03. 2018 07:24
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
↑ Ferdish:
Jak na to? A jak potom vyvodit něco z těch dvou výsledků?
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 14. 03. 2018 12:20
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
↑ Andrejka3:
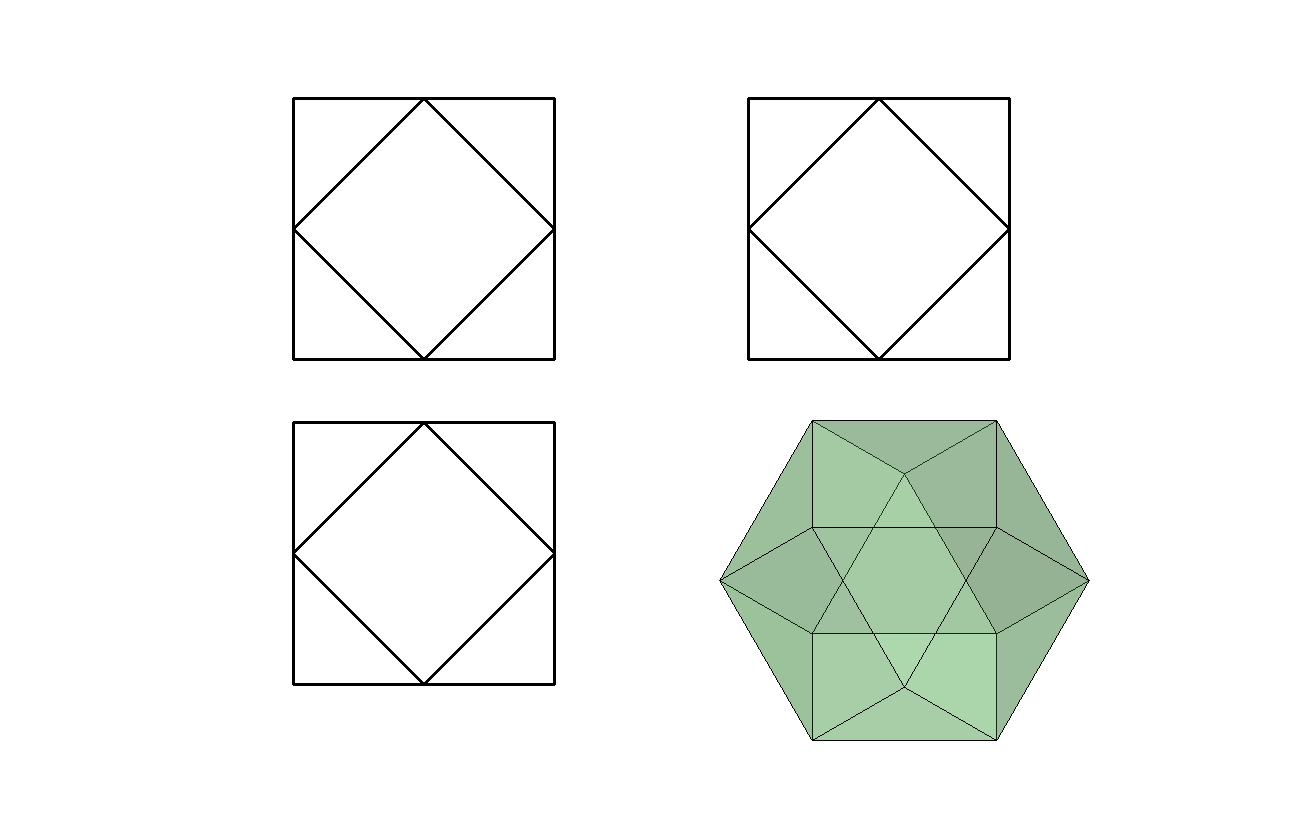
Takové těleso se nazývá "cuboctahedron".
Obrázek
Zkusil bych třeba jako poměr ploch (povrchů)(předpokládejme hrana=a=1)
Pak



Offline
#7 14. 03. 2018 13:33 — Editoval vanok (14. 03. 2018 18:16)
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
Pozdravujem ↑ Honzc: a tiez aj ↑ Andrejka3:,
To si myslel na https://en.m.wikipedia.org/wiki/Cuboctahedron.
Ale pozor. Taka obrezana kocka ma vsetki hrany rovnakej dlzky.
A tiez je dobre vyvazena, lebo ak sa nemylim vtedy aj vzdialenost vrcholov od centra objemu je taka ista ako dlzka hran.
Edit. Ako to potvrdil kolega Honzc ↑ Honzc:
Edit.
(Ake su ine stabilne situacie obrezanej kocky? Ine ako dva extremne pripady, povodnu kocku a uplne obrezanej kocky, co da pravidelny tetraeder.
Edit.
Dalsie stopy ako vysetrit stabilitu
Vdaka https://en.m.wikipedia.org/wiki/Stabili … 564203723.
No vsak neviem ako modelizovat taku situaciu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 14. 03. 2018 14:31 — Editoval Honzc (14. 03. 2018 14:36)
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
↑ vanok:
Však v zadání je, že rohy se ořezávají do poloviny hran
Pak takové těleso je popravidelné (Archimedes) těleso cuboctotahodron tvořené 8-mi rovnostrannými trojúhelníkovými plochami a 6-ti čtverci. Takové těleso má všechny hrany stejně dlouhé.
Dokonce když budeme řezat krychli o hraně délky a=sqrt(2) bude délka krany c. dlouhá c=1.
Něco ktomuto tělesu Tady
Opsaná koule má poloměr opravdu R=1, těžiště tělesa je v jejím středu.
Z toho jsem vycházel při výpočtu
Offline
#10 14. 03. 2018 16:38 — Editoval laszky (19. 03. 2018 22:50)
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
Ahoj, pokusil jsem se na to prijit takhle...
Spocital jsem energii, ktera je nutna k prevraceni kostky ze ctverce na trojuhelnik, resp. obracene. To mi vyslo

Takze by se zdalo, ze ctverec bude padat casteji, protoze k prevraceni na ctverec je zapotrebi mene energie.
Pak jsem se snazil vzit do uvahy kinetickou energii kostky. Pri prechodu z trojuhelnika na ctverec dojde ke zmene smeru rychlosti a ta by se mela zmensit.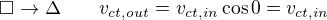
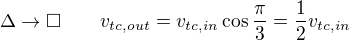
Tim padem se zmensi i kineticka energie a lze urcit rychlosti, pri kterych dojde k prevraceni na jednu stenu, ale na dalsi stenu uz se kostka neprevrati.
Ctverec tedy padne, pokud
Trojuhelnik padne pokud
Pro rychlosti to vychazi nasledovne.

Pokud je tedy tesne pred pritisknutim steny k podkladu rychlost v uvedenem rozmezi, kostka se jiz dale neprevrati, zaroven ale rychlost byla dostatecne velka, aby se kostka mohla na aktualni stenu prevratit. Ted by se mozna melo urcit jake je rozmezi pocatecnich rychlosti kostky a urcit z jake pocatecni rychlosti lze dospet do jednoho z uvedenych stavu (samozrejme pro idealni podklad a idealni "kostku" ktera neskace atd.).
Ale jelikoz nejsem fyzik, tak je taky mozny, ze jsem nekde napsal nesmysl :-)
Edit: Opravil jsem preklep ve dvou cislech.
Jeste dalsi uvahy:
Offline
#11 14. 03. 2018 17:00
#12 14. 03. 2018 17:56 Příspěvek uživatele check_drummer byl skryt uživatelem check_drummer. Důvod: Aha, to je zakázané. :-)
#13 14. 03. 2018 21:04
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
Offline
#14 14. 03. 2018 23:31
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
check_drummer: Tu závorku jsem psala speciálně kvůli Tobě, ale příště Ti to potěšení nevezmu :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#15 15. 03. 2018 00:18 Příspěvek uživatele laszky byl skryt uživatelem laszky.
#16 15. 03. 2018 20:21
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
Podle mě to určitě souvisí s tou energií, potřebnou k tomu, aby se kostka dostala z polohy "sedící na ploše" do polohy "na hraně", odkud se může zase převalit jinam.
Jen nevím, jestli pravděpodobnost bude lineárně úměrná té energii, nebo to bude spíš něco jako Boltzmanovo rozdělení
Pokud budou rohy seříznuté "dobře", aby energie na rohové ploše byla stejná jako na kostkové ploše, měla by být i pravděpodobnost stejná - krom samozřejmě toho, že rohů bylo 8, zatímco ploch jen 6.
Ale ještě je tam komplikace s tvarem těch ploch, jedny budou mít tvar trojúhelníka, jiné šestiúhelníka, takže závislost na směru rychlosti bude také jiná. Ale otázka je, jestli to má na něco vliv, protože třeba ve statistické mechanice (odkud pochází to Boltzmanovo rozdělení) závisí pravděpodobnost obsazení stavu jen na jeho energii, a tyhle podružné síly (co nekonají práci) nemají na nic vliv. Jenže je otázka, lze li tohle aplikovat na házení kostkou.
Pokud by se měla i kostka při vrhu řídit Boltzmanovou mechanikou, pak je to velmi jednoduché - pravděpodobnost stavu záleží jen na jeho energii (výšce těžiště nad podložkou), a to exponenciálně. Ale jak říkám, to platí pro stav tepelné rovnováhy, což kostka zrovna není.
Taky je možné že se to bude chovat jinak při házení na hladké (kluzké) podložce, jako třeba na povrchu stolu, a jinak třeba na stolu pokrytém gumou....já si popravdě nedokážu představit ani výpočet toho, jak dlouho se vydrží kostka po stole kutálet.
Offline
#17 15. 03. 2018 20:52
Re: Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
Andrejka3 napsal(a):
Pokud je ta kostka právě postavená na hranu a má nulovou rychlost, pak s 64% pravděpodobností spadne na čtverec. viz Wolfram
Nemáš k dispozici nějaké jednoduché fyzikální zdůvodnění, proč by to tak mělo být ?
Podle mě, pokud stojí kostka na hraně (že její těžiště je svisle nad tou hranou), bude tak stát navěky. Plyne to z 2. Newtonova zákona.
A pokud kostka nakonec na nějakou stranu spadne, tak je to buď proto, že nebyla postanevá úplně přesně, nebo proto, že na ni zapůsobila nějaká malinká síla, kterou jsme přehlédli - závan větru, zachvění podložky, prostě cokoliv.
V obou případech "ta věc" co způsobila pád kostky na konkrétní stranu vůbec nesouvisí s geometrií kostky samotné.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé a náročnější úlohy z fyziky
- » Hod mnohostěnem, pravděpodobnost, že padne jistá stěna
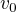 pocatecni rychlost kostky, dale
pocatecni rychlost kostky, dale  a
a  .
. , ze
, ze 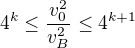 .
.  . V tom pripade je totiz
. V tom pripade je totiz  a na kostce doslo celkem k-krat k preklopeni z trojuhelnikove strany na ctvercovou + jedno dalsi preklopeni ze ctverce na trojuhelnik.
a na kostce doslo celkem k-krat k preklopeni z trojuhelnikove strany na ctvercovou + jedno dalsi preklopeni ze ctverce na trojuhelnik. , pak na kostce padne ctverec, nebot
, pak na kostce padne ctverec, nebot  a na kostce doslo celkem (k+1)-krat k preklopeni z trojuhelnikove strany na ctvercovou (tzn. kostka se diky o trochu vetsi rychlosti jeste jednou prevratila oproti predeslemu pripadu).
a na kostce doslo celkem (k+1)-krat k preklopeni z trojuhelnikove strany na ctvercovou (tzn. kostka se diky o trochu vetsi rychlosti jeste jednou prevratila oproti predeslemu pripadu). -krat casteji (ale klidne i
-krat casteji (ale klidne i  -krat, napr pri
-krat, napr pri  )
)