Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Derivace s kovariantními a kontravariantní indexy
#1 21. 03. 2018 08:48
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Derivace s kovariantními a kontravariantní indexy
Dobrý den,
měl bych otázku ohledně kovariantních a kontravariantních indexů v derivacích. Ve skriptech Kulhánka ( http://www.aldebaran.cz/studium/mechanika.pdf ), při odvození Lagrangeových rovnich z hustoty lagrangianu pro skalární pole (1.231), jedná se mi o zkrácený výpočet na str. 79 uvozený "... a ještě kratší řešení". V druhém kroku výpočtu je symbolická derivace součinu:

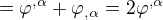
a k tomu mám otázku: je možné "pokrátit" derivace podle proměnné s horním indexem s derivací podle stejné proměnné se stejným indexem akorát dolním? A jde sečíst dva výrazy, když jeden má horní index a druhý dolní? Nebo je to jen v tomto případě definice hustoty lagrangianu přes čtyřgradienty skalárního pole? Chápu smysl zavedení kovariantních a kontravariantních indexů, ale nejsem moc kovaný v tom, co si s nimi mohu dovolit.
Děkuji
Bulušek
Offline
#2 21. 03. 2018 14:27
Re: Derivace s kovariantními a kontravariantní indexy
↑ Roscelinius:
Podle me proste jen zkratil ten predchozi vypocet do jednoho radku. Tam je videt, proc to tak vychazi ;-)
Offline
#4 21. 03. 2018 22:41
Re: Derivace s kovariantními a kontravariantní indexy
↑ MichalAld:
Nejsem zadnej expert, musel jsem si to trochu pripomenout, takze bych ti spis doporucil nekoho jinyho. :) Navic ty fyzikalni zapisy obecne jsou obcas (z matematickyho pohledu) trestny cin :-)
Offline
#5 22. 03. 2018 08:51 — Editoval Roscelinius (22. 03. 2018 11:24)
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Derivace s kovariantními a kontravariantní indexy
↑ laszky: Nemyslím si, že by to byl stejný výpočet, podle kontextu jsou to tři různé způsoby výpočtu. Navíc zadání je zde přeidexováno z μ na α bez přepočtu přes metriku g a Kroneckerovo delta δ .
Jde mi o to, jestli je správné interpretovat výpočet takto: ![kopírovat do textarea $\partial_{\alpha } [\frac{\partial L}{\partial \varphi _{,\alpha } }]- \frac{\partial L}{\partial \varphi }=$](/mathtex/4f/4fcf854260f7fc18a03d2ed4615442cb.gif)
![kopírovat do textarea $=\partial_{\alpha } [\frac{\partial (\frac{1}{2} \varphi _{,\alpha } \varphi ^{,\alpha }) }{\partial \varphi _{,\alpha } }]- \frac{\partial (\frac{1}{2} \varphi _{,\alpha } \varphi ^{,\alpha }) }{\partial \varphi }=$](/mathtex/4f/4f89ea3c67bd2a4ea09acc82a3bb557d.gif)

![kopírovat do textarea $= \frac{1}{2} \partial _{\alpha } [\frac{\partial (\varphi _{,\alpha })}{\partial \varphi ,_{\alpha }}\varphi ^{,\alpha } + \varphi _{,\alpha }\frac{\partial (\varphi ^{,\alpha })}{\partial \varphi ,_{\alpha }} ]=$](/mathtex/b4/b47960f70ae7d81e39ad4dae4eb02759.gif)
![kopírovat do textarea $= \frac{1}{2} \partial _{\alpha } [1\cdot \varphi ^{,\alpha } + \varphi _{,\alpha }\cdot 1 ]=$](/mathtex/21/2177f977e47a2ca727243ecd343df45a.gif)
![kopírovat do textarea $= \frac{1}{2} \partial _{\alpha } [2\cdot \varphi ^{,\alpha } ]=$](/mathtex/8f/8f5c066d4e0829744f0e307658ef16d0.gif)

Díky za reakce
Offline
#6 24. 03. 2018 11:35
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: Derivace s kovariantními a kontravariantní indexy
Kdyby snad někdo věděl a chtěl zareagovat, tak mě napadlo, co kdyby to šlo pomocí snížení a zvýšení indexů![kopírovat do textarea $\partial_{\alpha } [\frac{\partial L}{\partial \varphi _{,\alpha } }]- \frac{\partial L}{\partial \varphi }=$](/mathtex/4f/4fcf854260f7fc18a03d2ed4615442cb.gif)
![kopírovat do textarea $=\partial_{\alpha } [\frac{\partial (\frac{1}{2} \varphi _{,\alpha } \varphi ^{,\alpha }) }{\partial \varphi _{,\alpha } }]- \frac{\partial (\frac{1}{2} \varphi _{,\alpha } \varphi ^{,\alpha }) }{\partial \varphi }=$](/mathtex/4f/4f89ea3c67bd2a4ea09acc82a3bb557d.gif)

![kopírovat do textarea $= \frac{1}{2} \partial _{\alpha } [\frac{\partial (\varphi _{,\alpha })}{\partial \varphi ,_{\alpha }}\varphi ^{,\alpha } + \varphi _{,\alpha }\frac{\partial (\varphi ^{,\alpha })}{\partial \varphi ,_{\alpha }} ]=$](/mathtex/b4/b47960f70ae7d81e39ad4dae4eb02759.gif)
![kopírovat do textarea $= \frac{1}{2} \partial _{\alpha } [\frac{\partial (\varphi _{,\alpha })}{\partial \varphi ,_{\alpha }}\varphi ^{,\alpha } + \varphi ^{,\alpha }\frac{\partial (\varphi _{,\alpha })}{\partial \varphi ,_{\alpha }} ]=$](/mathtex/0c/0c25f638a74e52047f4adbee1b031ff2.gif)
-je možné povýšit nebo snížit indexy i v derivacích?
dál už by to bylo snadné:![kopírovat do textarea $= \frac{1}{2} \partial _{\alpha } [1\cdot \varphi ^{,\alpha } + \varphi ^{,\alpha }\cdot 1 ]=$](/mathtex/cc/ccfb437c67e1452a6bd90c836adec535.gif)
![kopírovat do textarea $= \frac{1}{2} \partial _{\alpha } [2\cdot \varphi ^{,\alpha } ]=$](/mathtex/8f/8f5c066d4e0829744f0e307658ef16d0.gif)

Odsouhlasil by mi někdo tyto úpravy? Děkuji
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Derivace s kovariantními a kontravariantní indexy
