Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Prázdninová limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#2 28. 07. 2009 14:56 — Editoval musixx (28. 07. 2009 16:17)
Re: Prázdninová limita posloupnosti
Offline
#3 28. 07. 2009 16:45
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita posloupnosti
Offline
#4 28. 07. 2009 17:13
Re: Prázdninová limita posloupnosti
Offline
#5 28. 07. 2009 17:34 — Editoval musixx (28. 07. 2009 17:47)
Re: Prázdninová limita posloupnosti
Při svém tápání jsem narazil na tohle. Když místo sinu použiju funkci 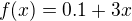 , tak vyjde (ověřeno jen hrubou silou, ale bude to tak):
, tak vyjde (ověřeno jen hrubou silou, ale bude to tak):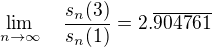
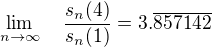
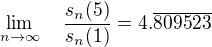
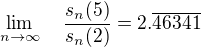
Mně tohle prostě přislo zajímavé, a tak jsem to sem musel připsat.
Je jasné, že pro 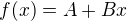 je
je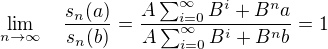 pro
pro  . Ale proč mi to vychází tak hezky racionální pro
. Ale proč mi to vychází tak hezky racionální pro  , tomu zatím vážně nerozumím (SW mi počítá s libovolnou přesností, takže tam ta periodicita snad nevzniká).
, tomu zatím vážně nerozumím (SW mi počítá s libovolnou přesností, takže tam ta periodicita snad nevzniká).
Offline
#6 28. 07. 2009 17:35
Re: Prázdninová limita posloupnosti
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#7 28. 07. 2009 17:58 — Editoval BrozekP (29. 07. 2009 10:19)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita posloupnosti
↑ lukaszh:
Navážu na tebe
Offline
#8 28. 07. 2009 18:43 — Editoval BrozekP (29. 07. 2009 10:23)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita posloupnosti
↑ musixx:
K tvé funkci 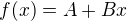 a limitě
a limitě  , kde
, kde 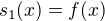 a
a 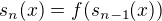 :
:
Není příliš těžké limitu pro  spočítat. Výsledek pro obecná A, B, a, b (kde
spočítat. Výsledek pro obecná A, B, a, b (kde  ) je
) je
Ať je to kompletní, tak
Offline
#9 29. 07. 2009 08:13 — Editoval Rumburak (29. 07. 2009 08:22)
Re: Prázdninová limita posloupnosti
Offline
#10 30. 07. 2009 13:58
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Prázdninová limita posloupnosti
Zdravím,
moc hezký příklad, řešením bohužel moc nerozumím, ale zřejmě souvisí s jedním problémem, na který jsem nedávno narazil, jde o rovnici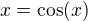 , kterou lze řešit standardními numerickými metodami, ale taky takhle:
, kterou lze řešit standardními numerickými metodami, ale taky takhle: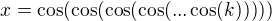 , kde
, kde  je reálné číslo. Můj dotaz je prostý: proč to vychází? :) jinými slovy (když se přidržím zápisu původního příkladu) proč je řešením $x=\lim_{n\rightarrow\infty}\cos_n(k)$, (v def. posloupnosti nahradíme sin za cos)
je reálné číslo. Můj dotaz je prostý: proč to vychází? :) jinými slovy (když se přidržím zápisu původního příkladu) proč je řešením $x=\lim_{n\rightarrow\infty}\cos_n(k)$, (v def. posloupnosti nahradíme sin za cos)
Offline
#11 30. 07. 2009 14:50 — Editoval musixx (30. 07. 2009 14:53)
Re: Prázdninová limita posloupnosti
↑ FliegenderZirkus: Banachův princip pevného bodu.
EDIT: Zkus Google pro podrobnosti.
Offline
#12 30. 07. 2009 16:11 — Editoval Rumburak (31. 07. 2009 10:44)
Re: Prázdninová limita posloupnosti
↑ FliegenderZirkus:
Ještě poznámka ke zmiňovanému Banachovu principu:
Pro funkci cos Banachova věta funguje, neboť pro libovolné počáteční  pak
pak 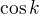 padne do uzavřeného intervalu [-1, 1 ] ,
padne do uzavřeného intervalu [-1, 1 ] ,
a rovněž další iterace v něm zůstanou, navíc na tomto intervalu fce f = cos splňuje podmínku  Banachovy věty
Banachovy věty
s kontrahující konstantou K < 1 (ostrá nerovnost) .
Stejnětak bychom mohli postupovat pro rovnici x = sin x , tedy hledat limitu posloupnosti iterací fce f = sin na libovolně danou počáteční hodnotu 
a dospěli bychom rovněž ke správnému řešení, a sice x = 0 , ale zde to Banachovou větou odůvodnit nelze, neboť v tomto případě
konstanta K < 1 (ostrá nerovnost) z předpokladů Banachovy věty neexistuje - muselo by se odůvodnění hledat jinak (nebo vzít vhodnou
jemnější větu o pevném bodě, než je Banachova).
Offline
#13 30. 07. 2009 18:05
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Prázdninová limita posloupnosti
Díky za rady, už hledám a studuju.
Offline
#14 05. 08. 2009 13:22
Re: Prázdninová limita posloupnosti
Řešení, které jsem našel společně s úlohou využívalo faktu, že pro dostatečně velká přirozená čísla  platí
platí
To se dokazovalo tím způsobem, že se našel docela snadný odhad funkce sinus pomocí Maclaurinvy řady. Je ale jasné, že řešení uvedené výše je výrazně snažší.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Prázdninová limita posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
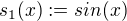
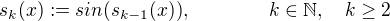 .
.  , kde
, kde
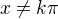 , tak (nehezky zapsáno)
, tak (nehezky zapsáno)  . Tedy by to mohlo svádět k použití l'Hospitala:
. Tedy by to mohlo svádět k použití l'Hospitala:  , což by mohlo svádět k tomu, že
, což by mohlo svádět k tomu, že  (
(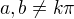 ).
).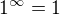 ".
".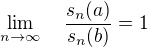 , když místo sinu použijeme v definici funkce
, když místo sinu použijeme v definici funkce 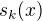 třeba libovolnou reálnou rostoucí funkci
třeba libovolnou reálnou rostoucí funkci  s
s 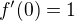 (analogicky pro klesající s derivací v nule rovnou -1), Mariáne?
(analogicky pro klesající s derivací v nule rovnou -1), Mariáne?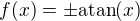 ,
, 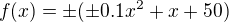 (s
(s 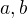 na nějakém vhodném okolí nuly, samozřejmě) atp. Jen ze zájmu jsem si to zkoušel na pár příkladech a mohlo by to platit.
na nějakém vhodném okolí nuly, samozřejmě) atp. Jen ze zájmu jsem si to zkoušel na pár příkladech a mohlo by to platit.
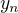 :-) Zatiaľ mám odhad: Postupnosť
:-) Zatiaľ mám odhad: Postupnosť 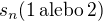 je klesajúca, potom
je klesajúca, potom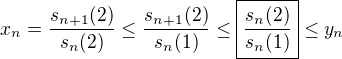
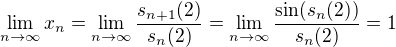
 , pak
, pak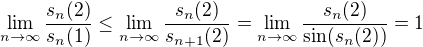 .
. (kde ještě dodefinuji
(kde ještě dodefinuji 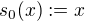 ) by (hádám) neměl být problém, za chvíli to sem dám, pokud nenarazím na nějakou překážku.
) by (hádám) neměl být problém, za chvíli to sem dám, pokud nenarazím na nějakou překážku.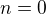 jistě platí
jistě platí  . Předpokládejme, že
. Předpokládejme, že  . Funkce sinus je na intervalu, který nás zajímá, rostoucí, takže
. Funkce sinus je na intervalu, který nás zajímá, rostoucí, takže  , to je ale to samé jako
, to je ale to samé jako 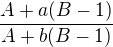
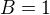 vyjde limita 1 a pro
vyjde limita 1 a pro 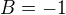 existuje limita pouze pokud
existuje limita pouze pokud 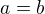 , limita je tedy také 1.
, limita je tedy také 1.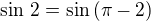 ,
,  ,
,  , takže
, takže  a dále
a dále .
.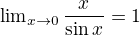 .
.