Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#6 27. 04. 2018 10:06 — Editoval Ferdish (27. 04. 2018 10:07)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Reálná a imaginární složka komplexního čísla
↑ kotry:
Len drobná poznámka.
Pri separátnom zápise zložiek komplexného čísla 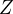 sa uplatňujú zaužívané označenia
sa uplatňujú zaužívané označenia  a
a  , pričom imaginárna zložka sa zvykne písať bez imaginárnej jednotky.
, pričom imaginárna zložka sa zvykne písať bez imaginárnej jednotky.
Offline
#11 05. 06. 2018 12:42
Re: Reálná a imaginární složka komplexního čísla
 ↑ vlado_bb:
somozřejmě je to fce(opraveno)
$" class="tex" onclick="zkopirujTex(this.alt, 'm')" title="kopírovat do textarea">f(z)=e^{5}\cdot i\cdot cos(3) = e^{5}\cdot i\cdot sin(\frac{6+\pi }{2})
↑ vlado_bb:
somozřejmě je to fce(opraveno)
$" class="tex" onclick="zkopirujTex(this.alt, 'm')" title="kopírovat do textarea">f(z)=e^{5}\cdot i\cdot cos(3) = e^{5}\cdot i\cdot sin(\frac{6+\pi }{2}) Ref(z)=e^{5}
Ref(z)=e^{5} Imf(z)=e^{5}\cdot sin(\frac{6+\pi }{2})
Imf(z)=e^{5}\cdot sin(\frac{6+\pi }{2})
$
Offline
 a
a  ?
? 



 , když roznásobíš závorku.
, když roznásobíš závorku. a imaginární složka je
a imaginární složka je 




 nemoze byt. Navyse, co je vlzstne
nemoze byt. Navyse, co je vlzstne  ? Ten prvy vyraz v prvom riadku, alebo ten druhy?
? Ten prvy vyraz v prvom riadku, alebo ten druhy?
 .
.