Matematické Fórum

Zeck · 24. 05. 2018 20:15

Dobrý den,

chtel bych vás požádat o pomoc s rešením nasledujícího problému:
V zadání je uvedeno: Zformulujte daný problém ve slabém smyslu jako a(u,v)=L(v). Zvolte testovací funkci v, prenásobte rovnici touto testovací funkci, zintegrujte pres \Omega , užijte Greenovu vetu a okrajové podmínky.
Okrajové podmínky:
a) $u = u_{D}$ ,
b) $\frac{\partial u}{\partial n}=0$ na $\Gamma _{N}$ ,
c) $-\varepsilon \frac{\partial u}{\partial n}=\alpha (u-\psi )$ na $\Gamma _{Z}$ .

$u_{D}=80, \alpha = 3, \psi =7, \varkappa =1, \varepsilon =0,01$

Kdyby mi někdo pomohl s tímhle, další bych už zvládl sám.

$-\nabla\cdot (\varepsilon \nabla u)+\varkappa u = f$

Rozepsal jsem to, ale nevím jak postupovat dál:
$-\frac{\partial }{\partial x} \left( \varepsilon \left( \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y} \right) \right)- \frac{\partial }{\partial x} \left( \varepsilon \left( \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y} \right) \right) + \varkappa u = f$

laszky · 24. 05. 2018 22:11 — Editoval laszky (16. 07. 2022 00:19)

↑ Zeck:

Ahoj, predpokladam, ze to a) plati na $\Gamma_D$ .

Pak uvazuj prostor $V=\{v\in H^1(\Omega), v=0\ \mbox{na}\ \Gamma_D \}$

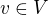Rovnici $-\mbox{div}(\varepsilon \nabla u)+\varkappa u = f$ prenasobis libovolnou funkci $v\in V$ a integrujes pres $\Omega$ , ziskas

$\int_{\Omega}-\mbox{div}(\varepsilon \nabla u)v\;\mbox{d}x +\int_{\Omega}\varkappa uv\;\mbox{d}x = \int_{\Omega}fv\;\mbox{d}x$ .

Na prvni integral pouzijes Greenovu vetu (resp. vetu o divergenci), coz je vicerozmerna analogie metody per partes:

$\int_K \mbox{div}\boldsymbol{g}\; \mbox{d}x = \int_{\partial K} \boldsymbol{g}\cdot\boldsymbol{n} \; \mbox{d}s$ , v tomto pripade

[mathjax] {\displaystyle \int_{\Omega} \mbox{div}(\varepsilon \nabla u)v + \varepsilon \nabla u\cdot\nabla v\; \mbox{d}x = \int_{\Omega} \mbox{div}(\varepsilon v\nabla u)\; \mbox{d}x = \int_{\partial \Omega} \varepsilon v\nabla u\cdot\boldsymbol{n} \; \mbox{d}s = \int_{\partial \Omega} \varepsilon v \, \frac{\partial u}{\boldsymbol{n}} \; \mbox{d}s } [/mathjax]

Rovnici tedy upravime na

[mathjax] {\displaystyle \int_{\Omega}\varepsilon \nabla u\cdot\nabla v\;\mbox{d}x - \int_{\partial \Omega} \varepsilon v \, \frac{\partial u}{\boldsymbol{n}} \; \mbox{d}s +\int_{\Omega}\varkappa uv\;\mbox{d}x = \int_{\Omega}fv\;\mbox{d}x}[/mathjax]

Hranicni integral upravime na

[mathjax] {\displaystyle \int_{\partial \Omega} \varepsilon v \, \frac{\partial u}{\boldsymbol{n}} \; \mbox{d}s = \int_{\Gamma_D} \varepsilon \underbrace{v}_{=0} \, \frac{\partial u}{\boldsymbol{n}} \; \mbox{d}s + \int_{\Gamma_N} \varepsilon v \, \underbrace{\frac{\partial u}{\boldsymbol{n}}}_{=0} \; \mbox{d}s + \int_{\Gamma_Z} \varepsilon v \, \frac{\partial u}{\boldsymbol{n}} \; \mbox{d}s = } [/mathjax]
[mathjax] {\displaystyle = \int_{\Gamma_Z} \varepsilon v \, \frac{\partial u}{\boldsymbol{n}} \; \mbox{d}s = -\int_{\Gamma_Z} v \, \alpha(u-\psi) \; \mbox{d}s } [/mathjax], proto je vysledny tvar rovnice

[mathjax] {\displaystyle \int_{\Omega}\varepsilon \nabla u\cdot\nabla v\;\mbox{d}x +\int_{\Gamma_Z} v \, \alpha(u-\psi) \; \mbox{d}s +\int_{\Omega}\varkappa uv\;\mbox{d}x = \int_{\Omega}fv\;\mbox{d}x } [/mathjax], nebol-li

[mathjax] {\displaystyle \int_{\Omega}\varepsilon \nabla u\cdot\nabla v\;\mbox{d}x +\int_{\Gamma_Z} \alpha\,u v \; \mbox{d}s +\int_{\Omega}\varkappa uv\;\mbox{d}x = \int_{\Omega}fv\;\mbox{d}x + \int_{\Gamma_Z} \alpha\,\psi v\; \mbox{d}s } [/mathjax]

Takze

[mathjax] {\displaystyle a(u,v) = \int_{\Omega}\varepsilon \nabla u\cdot\nabla v\;\mbox{d}x +\int_{\Gamma_Z} \alpha\,u v \; \mbox{d}s +\int_{\Omega}\varkappa uv\;\mbox{d}x } [/mathjax]
[mathjax] {\displaystyle L(v) = \int_{\Omega}fv\;\mbox{d}x + \int_{\Gamma_Z} \alpha\,\psi v\; \mbox{d}s } [/mathjax]

a slaba formulace zni:

Najdete funkci $u\in H^1(\Omega)$ takovou, ze plati

a) $u=u_D\quad \mbox{na}\ \Gamma_D\ \mbox{ve smyslu stop}$
b) $a(u,v)=L(v)\quad \mbox{pro vsechna}\ v \in V$

Zeck · 25. 05. 2018 08:33

↑ laszky:

Diky, musim si to doma projít sám, abych tomu rozuměl.
Ještě jednou děkuji a přeji hezký den. :-)

Zeck · 27. 05. 2018 00:07 — Editoval Zeck (27. 05. 2018 13:52)

Chtěl by vás ještě požádat o kontrolu a pomoc. Vyžaduje se ještě ověření, zda pro danou slabou formulaci existuje řešení užitím Lax-Milgramovy věty a následně nájdení Galerkinovy aproximace $u_{h}$ pomoci řešení soustavy lineárních rovnic. Definici L-M věty mám a snažil jsem se to udělat, ale nevím jak najít Galerkinovou aproximaci, proto bych vás chtěl požádat o pomoc.

Linearita:
$L(v_{1}+v_{2})=\int_{\Omega }^{}f(v_{1}+v_{2}) \mathrm{d}x+\int_{\Gamma_{Z} }^{}\alpha \psi (v_{1}+v_{2}) \mathrm{d}s=\int_{\Omega }^{}fv_{1}+fv_{2} \mathrm{d}x+\int_{\Gamma_{Z} }^{}\alpha \psi v_{1}+\alpha \psi v_{2} \mathrm{d}s=$
$=\int_{\Omega }^{}fv_{1} \mathrm{d}x+\int_{\Gamma_{Z} }^{}\alpha \psi v_{1} \mathrm{d}s+\int_{\Omega }^{}fv_{2} \mathrm{d}x+\int_{\Gamma_{Z} }^{}\alpha \psi v_{2} \mathrm{d}s=L(v_{1})+L(v_{2})$

Bilinearita:
$a(u_{1}+u_{2},v)=\int_{\Omega }^{}\varepsilon \nabla (u_{1}+u_{2})\nabla v \mathrm{d}x+\int_{\Gamma _{Z} }^{}\alpha (u_{1}+u_{2}) v\mathrm{d}s+\int_{\Omega }^{}\varkappa (u_{1}+u_{2}) v \mathrm{d}x=$

$=\int_{\Omega }^{}\varepsilon \nabla u_{1}\nabla v \mathrm{d}x+\int_{\Gamma _{Z} }^{}\alpha u_{1}v \mathrm{d}s+\int_{\Omega }^{}\varkappa u_{1}v \mathrm{d}x+\int_{\Omega }^{}\varepsilon \nabla u_{2}\nabla v \mathrm{d}x+\int_{\Gamma _{Z} }^{}\alpha u_{2}v \mathrm{d}s+\int_{\Omega }^{}\varkappa u_{2}v \mathrm{d}x=a(u_{1},v)+a(u_{2},v)$

V-eliptičnost:
$a(u,u) = \int_{\Omega }^{}\varepsilon |u|^{2}_{1,\Omega} v \mathrm{d}x+\int_{\Gamma _{Z} }^{}\alpha u^{2} \mathrm{d}s+\int_{\Omega }^{}\kappa u^{2} \mathrm{d}x \ge \varepsilon |u|^{2}_{1,\Omega} \mathrm{d}x+\kappa u^{2} \mathrm{d}x \int_{\Gamma _{Z} }^{}\alpha u^{2} \mathrm{d}s\ge min(\varepsilon ,\varkappa _{0}) \parallel u \parallel^{2}_{1.\Omega }$

Stačí to jako důkaz, že existuje řešení?

laszky · 27. 05. 2018 10:05 — Editoval laszky (28. 05. 2018 01:06)

↑ Zeck:

Ahoj, linearita $L$ je dobre, bilinearita $a$ neni dobre - chybi linearita v druhe slozce. Elipticita neni dobre:
$|u|^2_{1,\Omega} = \int_{\Omega}|\nabla u(x)|^2\,\mathrm{d}x$ , takze $\int_{\Omega}|u|^2_{1,\Omega}\,\mathrm{d}x$ nedava smysl a cely ten posledni radek asi obsahuje radu preklepu ;-)

Dale ti chybi ukazat, ze:

$a(u,v)\leq C\|u\|_{1,\Omega}\|v\|_{1,\Omega}$

a

$L \in V'$

Zeck · 27. 05. 2018 23:18

Ahoj,

snažil jsem se to upravit, je to lepší? Je to pro mně nové a nemám s tím zkušenosti. Ta předposlední rovnice je Cauchy-Schwarzova nerovnost?
$a(u,v)\leq C\|u\|_{1,\Omega}\|v\|_{1,\Omega}$
Pokud ano, tak o to jsem se pokusil.
Ale toto bohužel vůbec nevím jak se dokazuje, ani jsem to nemohl najít ve svých materiálech. :-(
$L \in V'$

Bilinearita:
$a(u_{1}+u_{2},v)=\int_{\Omega }^{}\varepsilon \nabla (u_{1}+u_{2})\nabla v \mathrm{d}x+\int_{\Gamma _{Z} }^{}\alpha (u_{1}+u_{2}) v\mathrm{d}s+\int_{\Omega }^{}\varkappa (u_{1}+u_{2}) v \mathrm{d}x=$

$=\int_{\Omega }^{}\varepsilon \nabla u_{1}\nabla v \mathrm{d}x+\int_{\Gamma _{Z} }^{}\alpha u_{1}v \mathrm{d}s+\int_{\Omega }^{}\varkappa u_{1}v \mathrm{d}x+\int_{\Omega }^{}\varepsilon \nabla u_{2}\nabla v \mathrm{d}x+\int_{\Gamma _{Z} }^{}\alpha u_{2}v \mathrm{d}s+\int_{\Omega }^{}\varkappa u_{2}v \mathrm{d}x=a(u_{1},v)+a(u_{2},v)$

V-eliptičnost:
$a(u,u) =\int_{\Omega }^{}\varepsilon \nabla u\nabla u \mathrm{d}x+\int_{\Gamma_Z }^{}\alpha u u \mathrm{d}s+\int_{\Omega }^{}\varkappa u u \mathrm{d}x =\varepsilon |\nabla u|^{2}_{1,\Omega} v \mathrm{d}x+\alpha |u|^{2}_{1,\Gamma_Z}+\varkappa |u|^{2}_{1,\Omega} \mathrm{d}x \ge min(\varepsilon ,\varkappa _{0}) \parallel u \parallel^{2}_{1.\Omega }$

Využití Cauchy-Scharzovy nerovnosti:
$|a(u,v)|=\int_{\Omega}\varepsilon \nabla u\cdot\nabla v\;\mbox{d}x +\int_{\Gamma_Z} \alpha\,u v \; \mbox{d}s +\int_{\Omega}\varkappa uv\;\mbox{d}x\le$

$\le \left(\int_{\Omega }^{}\varepsilon |\nabla u|^{2} \mathrm{d}x \right)^{\frac{1}{2}}\left(\int_{\Omega }^{} |\nabla v|^{2}\mathrm{d}x\right)^{\frac{1}{2}}+\left(\int_{\Gamma_{Z} }^{}\alpha | u|^{2}\mathrm{d}s\right)^{\frac{1}{2}}\left(\int_{\Gamma_{Z} }^{} | v|^{2}\mathrm{d}s\right)^{\frac{1}{2}}+\left(\int_{\Omega }^{}\varepsilon | u|^{2}\mathrm{d}x\right)^{\frac{1}{2}}\left(\int_{\Omega }^{} | v|^{2}\mathrm{d}x\right)^{\frac{1}{2}}$

$|L(v)|=|\int_{\Omega }^{} fv \mathrm{d}x+\int_{\Gamma_Z }^{} \alpha \psi v \mathrm{d}s| \le \left( \int_{\Omega }^{}|f|^{2} \mathrm{d}x \right)^{\frac{1}{2}} \left( \int_{\Omega }^{}|v|^{2} \mathrm{d}x \right)^{\frac{1}{2}} + \left( \int_{\Gamma_Z }^{} \alpha \psi |v|^{2} \mathrm{d}s \right)^{\frac{1}{2}}$

Bati · 28. 05. 2018 00:04

↑ Zeck:
ano, Cauchy-Schwartz, nebo obecne Holderova nerovnost, pokud bys nemel Hilbertovy prostory. Potrebujes tam jeste odhadnout ty okrajove cleny a na to muzes pouzit vetu o stopach: $\|u\|_{L^2(\partial\Omega)}\leq c \|u\|_{H^1(\Omega)}$

laszky · 28. 05. 2018 02:26 — Editoval laszky (28. 05. 2018 23:34)

↑ Zeck:

Ahoj, spravne je to takto:

Elipticita (=koercivita) $a$ :

$a(v,v) = \varepsilon | v|^{2}_{1,\Omega} + \alpha \|v\|^{2}_{0,\Gamma_Z}+\varkappa \|v\|^{2}_{0,\Omega} \geq \min(\varepsilon ,\varkappa) \| v \|^{2}_{1,\Omega }$

Omezenost $a$ :

$a(u,v) =\int_{\Omega}\varepsilon \nabla u\cdot\nabla v\;\mbox{d}x +\int_{\Gamma_Z} \alpha\,u v \; \mbox{d}s +\int_{\Omega}\varkappa uv\;\mbox{d}x\leq \varepsilon |u|_{1,\Omega}|v|_{1,\Omega} + \alpha \|u\|_{0,\Gamma_Z} \|v\|_{0,\Gamma_Z} + \varkappa\|u\|_{0,\Omega}\|v\|_{0,\Omega} \leq$
$\leq \varepsilon |u|_{1,\Omega}|v|_{1,\Omega} + \alpha \|u\|_{0,\partial\Omega} \|v\|_{0,\partial\Omega} + \varkappa\|u\|_{0,\Omega}\|v\|_{0,\Omega} \leq (\max\{\varepsilon,\varkappa\}+ \alpha C_T^2 ) \|u\|_{1,\Omega} \|v\|_{1,\Omega}$ ,

kde se vyuzilo nerovnosti

$\|w\|_{0,\partial\Omega} \leq C_T \|w\|_{1,\Omega}$ (veta o stopach) a

$|u|_{1,\Omega}|v|_{1,\Omega} + \|u\|_{0,\Omega}\|v\|_{0,\Omega} \leq \|u\|_{1,\Omega} \|v\|_{1,\Omega}$ (plyne z definice normy $\|w\|^2_{1,\Omega} = |w|^2_{1,\Omega} + \|w\|^2_{0,\Omega}$ )

Spojitost (=omezenost) funkcionalu L, tzn. $L\in V'$

$|L(v)| \; = \; \left| \int_{\Omega}fv\;\mbox{d}x + \int_{\Gamma_Z} \alpha\,\psi v\; \mbox{d}s \right| \; \leq \;\|f\|_{0,\Omega}\|v\|_{0,\Omega} + \|\alpha\psi\|_{0,\Gamma_Z}\|v\|_{0,\Gamma_Z} \; \leq$
$\leq \; \|f\|_{0,\Omega}\|v\|_{1,\Omega} + \alpha\psi\,|\Gamma_Z|\,\|v\|_{0,\partial\Omega} \; \leq \; \bigr(\|f\|_{0,\Omega}+\alpha\psi C_T\,|\Gamma_Z|\,\bigr)\|v\|_{1,\Omega}$

EDIT: Z uvedenych odhadu vyplyva, ze existuje-li $\widetilde{u}_D\in H^1(\Omega)$ takova, ze $\widetilde{u}_D=u_D$ na $\Gamma_Z$ ve smyslu stop, potom $u-\widetilde{u}_D\in V$ a

$\min(\varepsilon ,\varkappa) \|u-\widetilde{u}_D\|^{2}_{1,\Omega } \; \leq \; a(u-\widetilde{u}_D,u-\widetilde{u}_D) \; = \; L(u-\widetilde{u}_D) - a(\widetilde{u}_D,u-\widetilde{u}_D) \; \leq$
$\leq \; \bigr(\|f\|_{0,\Omega}+\alpha\psi C_T\,|\Gamma_Z|\,\bigr)\|u-\widetilde{u}_D\|_{1,\Omega} + (\max\{\varepsilon,\varkappa\}+ \alpha C_T^2 ) \|\widetilde{u}_D\|_{1,\Omega} \|u-\widetilde{u}_D\|_{1,\Omega} \; =$ .
$=\; \Bigr[\|f\|_{0,\Omega}+\alpha\psi C_T\,|\Gamma_Z| + (\max\{\varepsilon,\varkappa\}+ \alpha C_T^2 ) \|\widetilde{u}_D\|_{1,\Omega} \Bigr] \; \|u-\widetilde{u}_D\|_{1,\Omega}$

Takze $\|u-\widetilde{u}_D\|_{1,\Omega} \; \leq \; \frac{\|f\|_{0,\Omega}+\alpha\psi C_T\,|\Gamma_Z| + (\max\{\varepsilon,\varkappa\}+ \alpha C_T^2 ) \|\widetilde{u}_D\|_{1,\Omega}}{\min(\varepsilon ,\varkappa)}$ , a proto

$\|u\|_{1,\Omega} \; \leq \; \|u-\widetilde{u}_D\|_{1,\Omega} + \|\widetilde{u}_D\|_{1,\Omega} \; \leq \; \frac{\|f\|_{0,\Omega}+\alpha\psi C_T\,|\Gamma_Z| + (\max\{\varepsilon,\varkappa\}+ \alpha C_T^2 ) \|\widetilde{u}_D\|_{1,\Omega}}{\min(\varepsilon ,\varkappa)} + \|\widetilde{u}_D\|_{1,\Omega}$ .

Z toho vyplyva, ze je-li prava strana teto nerovnosti definovana ( $f$ a $\widetilde{u}_D$ jsou dostatecne regularni, tj. $f\in L^2(\Omega)$ a $\widetilde{u}_D\in H^1(\Omega)$ ) , potom i $u\in H^1(\Omega)$ .

Zeck · 28. 05. 2018 21:20

↑ laszky:

Děkuji za pomoc. :-)

Zeck · 14. 06. 2018 19:20

Chtěl bych se ještě zeptat na Galerkinovou aproximaci daného problému. V mých materiálech mám napsané metody standardní a modifikované - Klasická metoda umelé vazkosti, Streamline diffusion a Streamline Upwind metoda. Jenom že s tímhle nemám žádne zkušenosti a nevím která metoda je vhodná. Z toho důvodu bych vás chtěl poprosit, pomohli by jste mi vybrat vhodnú metodu a ukázali, jak se prakticky aplikuje na můj problém?

laszky · 14. 06. 2018 22:52

↑ Zeck:

V tomto pripade cokoli streamline pouzit nelze, protoze se jedna o reakcne-difuzni rovnici neobsahujici zadne konvektivni pole, a tedy proudnice zde nenajdes. Pouzij obycejnou Galerkinovu metodu konecnych prvku ;-)

Matematické Fórum

#1 24. 05. 2018 20:15

Formulace problemu ve slabém smyslu

#2 24. 05. 2018 22:11 — Editoval laszky (16. 07. 2022 00:19)

Re: Formulace problemu ve slabém smyslu

#3 25. 05. 2018 08:33

Re: Formulace problemu ve slabém smyslu

#4 27. 05. 2018 00:07 — Editoval Zeck (27. 05. 2018 13:52)

Re: Formulace problemu ve slabém smyslu

#5 27. 05. 2018 10:05 — Editoval laszky (28. 05. 2018 01:06)

Re: Formulace problemu ve slabém smyslu

#6 27. 05. 2018 23:18

Re: Formulace problemu ve slabém smyslu

#7 28. 05. 2018 00:04

Re: Formulace problemu ve slabém smyslu

#8 28. 05. 2018 02:26 — Editoval laszky (28. 05. 2018 23:34)

Re: Formulace problemu ve slabém smyslu

#9 28. 05. 2018 21:20

Re: Formulace problemu ve slabém smyslu

#10 14. 06. 2018 19:20

Re: Formulace problemu ve slabém smyslu

#11 14. 06. 2018 22:52

Re: Formulace problemu ve slabém smyslu

Zápatí